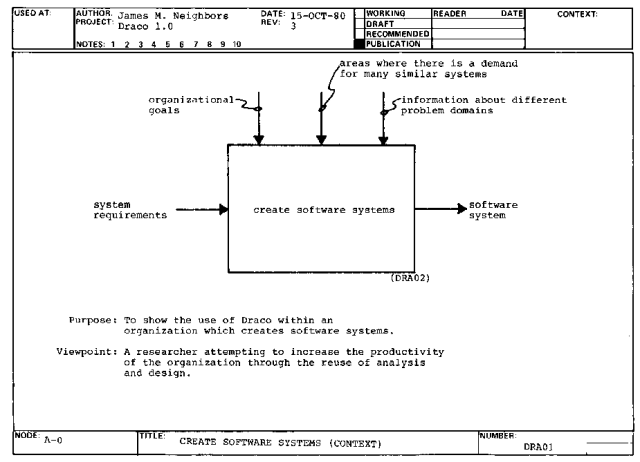
Figure 2. A-0 Create Software Systems (Context)
It is the thesis of this work that many computer software systems being built today are similar and should be built out of reusable software components.
The appropriate use of software components is investigated by analogy to the classical engineering question of whether to build an object out of custom-made parts or standard parts and assemblies. The same analogy is used to explain some of the problems with previous work on reusable software. The result of reasoning with the engineering analogy is that the reuse of software results only from the reuse of analysis, design, and code; rather than just the reuse of code.
The concept of domain analysis is introduced to describe the activity of identifying the objects and operations of a class of similar systems in a particular problem domain. A domain analysis is represented by a domain-specific language, a prettyprinter, source-to-source transformations, and software components.
A domain's software components map statements from the domain into other domains which are used to model the objects and operations of the domain. Software components represent implementation choices. The components are managed using a module interconnection language to insure usage constraints.
The source-to-source transformations represent domain-specific optimizations, independent of any implementation, which are used to optimize statements in the domain. The transformations are useful primarily when the domain is used as a modeling domain. A method of automatically producing metarules for a set of transformations is described. The metarules remove the burden of having to suggest individual transformations from the user.
A formal model of the usage constraints and modeling possibilities of a set of domains is presented. It is shown that the reusability question ("Can a particular domain-specific program be refined into an executable language using a given a set of domains?") can be answered using the formal model.
Experiments using a prototype system, Draco 1.0, which embodies the concepts described, are presented and the results discussed. The largest example results in approximately 20 pages of source code and uses eight modeling domains. Each object and operation in the resulting program may be explained by the system in terms of the program specification.
Related work in the areas of automatic programming, program generation, programming languages, software engineering, and transformation systems is presented.
Finally, some future work in this area is outlined.
Each year more than $50,000,000,000 are spent on software production and evolution in the United States [Lehman80]. The traditional term of "maintenance" for all work on a software system after it is initially constructed is misleading. We prefer the term "evolution" after [Lehman80, Scacchi80, vanHorn80] to denote the repair, adaptation, and enhancement of a software system. This huge sum is spent on something which cannot be seen, felt, touched, tasted or heard in the conventional sense. The intangible nature of software has caused much of the problem in its production. There is no sense feedback in the production of software. Over the past years, the problem of software production has been growing rapidly with the increased size of software systems. Today "personal computers" threaten to be able to hold the largest software systems built. Unless techniques to create software increase dramatically in productivity, the future of computing will be very large software systems barely being able to use a fraction of the computing power of extremely large computers.
By "software crisis," we mean that there is a demand for quality software which cannot be met with present methods of software construction. The judgement as to whether the software is needed or whether more software is better is not made here. Some of the points which have brought about the software crisis are listed below:
This dissertation describes a software production technique based on the concept of parts and assemblies. The concept has been very successful in the production of standardized objects such as computer hardware. It is the goal of this work to increase software construction productivity as a partial answer to the software crisis.
The beginning of the software crisis was heralded by the failure of some very large software systems to meet their analysis goals and delivery dates in the 1960's. These systems failed regardless of the amount of money and manpower allocated to the projects. These failures led to a conference on the problem of software construction which marked the beginning of software engineering [Buxton76]. Studies of the process of software construction have identified the phases that a software project goes through and these phases have been combined into a model called the software lifecycle.
If we view the lifetime of a software system as consisting of the phases requirements analysis, design, coding, integration and testing, and evolution, then typical costs of the different phases [Brooks74, Boehm73] excluding requirements analysis are shown in figure 1. This early view of the lifecycle serves our purpose here but it is important to note that more recent views of the lifecycle [Kerola81, Scacchi80] are more sensitive to the needs of the organization requesting the system, the dynamics of the organization building the system, and the information processing abilities of the people developing the system.
9% design
6% coding
15% integration and testing
70% evolution
It is difficult to test high-impact tools for software production for three reasons. One reason is that the tools are used in a complex social setting where not all the users are motivated by a desire for high software production. A second reason is that producing software is very expensive and the data collection required is an added expense to an already expensive process. The third difficulty in testing high-impact tools is that there are no really good system quality metrics with which to judge the resulting system built using the tool. It is difficult to judge the worth of the resulting system to the organization which desired it. Many requests for "maintenance" on a completed system may mean either that the system was built poorly with many errors or that it was built well enough that the users see enhancements which could make a good system even better.
The software production technique described in this dissertation is, in our view, a high-impact tool which inherits the difficulties of testing mentioned above. We have not attempted to statistically verify an increase in software productivity or judge the "goodness" of the systems resulting from the use of the tool. Such a study should be a requirement before any technique is ever used in production.
The idea of using standard parts and forming them into assemblies is a very old idea.
"Eli Whitney of New Haven Conn. received an order for a large number of guns in 1789. Instead of hiring a large number of individual gunsmiths, he designed interchangeable parts and made jigs and fixtures so that relatively unskilled people could make the parts. He missed his delivery schedule, but he is credited with having invented the parts-and-assemblies approach with re-usable parts. The principles and techniques of the parts-and-assemblies approach have since become well known, and automated support for the documentation exists throughout industry." [Edwards74]The parts-and-assemblies approach has been used extensively in engineering and is one of the techniques which has enabled computer hardware engineers to increase the power and capacity of computers in a short time. Henry Ford combined the idea of parts and assemblies with the idea of an assembly line to make model-T Fords. It is important here to understand that the parts-and-assemblies idea does not infer the use of assembly lines.
There are two basic approaches to building things. The craftsman approach relies on a highly skilled craftsman to build an object from raw materials. The raw materials are fashioned into custom parts and fitted together to form custom assemblies. The parts-and-assemblies approach relies on already built standard parts and standard assemblies of parts to be combined to form the object. Each of the approaches has its good and bad points.
With the craftsman approach, the custom parts and assemblies are tailored to the specific problem at hand. These custom parts represent a very efficient implementation; probably better than could be built from standard parts. Given the time, a craftsman always builds a better object than one constructed from standard parts. By "better" here we mean more responsive to the goals of construction [Alexander64]. The craftsman approach has its drawbacks in that craftsmen are expensive to employ and hard to find. Any system built by a craftsman is a custom system and will require custom maintenance. This means that the maintenance must be done by a craftsman who must shape new custom parts to fit with the old custom parts in an object.
The parts-and-assemblies approach offers cheaper construction costs since the object is built from pre-built standard parts. An assembly is a structure of standard parts which cooperate to perform a single function. The use of standard parts and assemblies will supply some knowledge about the failure modes and limits of the parts. This information is unavailable with custom parts. Use of standard parts also creates a language for discussion of future objects and extensions to objects currently under construction. The parts-and-assemblies approach has its drawbacks in that the design of useful standard parts and assemblies is very expensive work and requires craftsman experience. Also, once a set of standard parts is created it may not suffice to construct all the objects desired.
From a different viewpoint, an assembly is a part.
"We understand complex things by systematically breaking them into successively simpler parts and understanding how these parts fit together locally. Thus, we have different levels of understanding, and each of these levels corresponds to an abstraction of the detail at the level it is composed from. For example, at one level of abstraction, we deal with an integer without considering whether it is represented in binary notation or two's complement, etc., while at deeper levels this representation may be important. At more abstract levels the precise value of the integer is not important except as it relates to other data." [Knuth74]Thus, an assembly at a different level of abstraction becomes a part. This idea will become important later when we discuss the problems encountered by previous work on software parts.
From the discussion of the pros and cons of the craftsman and the parts-and-assemblies approaches, it is apparent that the parts-and-assemblies approach is appropriate only to those situations where many similar objects are to be built. Otherwise, the cost of producing the standard parts by a craftsman is much greater than the cost saved by using standard parts. If an object to be built is a one-of-a-kind custom object it should be built by a craftsman; otherwise it should be determined if the parts-and-assemblies approach could be cost effective.
Historically, software construction has taken the craftsman approach. In the early days of computing, the software systems were one-of-a-kind and the craftsman approach was the natural approach. Today quite a few software systems being built by the craftsman approach are similar. In particular, the construction of system software (text editors, assemblers, compilers, etc.), business data processing systems (inventory, accounting, billing, etc.), and simple process control systems are all areas where many thousands of similar systems exist. It is not at all clear that the constructors of these systems are craftsmen. In fact, with the rapidly increasing numbers of analysts and programmers [Lientz80] it is doubtful that the constructors of these systems are craftsmen. In our view, the high cost of custom software systems has never been clearly represented since the use of standard parts and assemblies to build low-cost systems has not been an alternative.
Historically, hardware construction has taken the parts-and-assemblies approach. Even though early computers were one-of-a-kind, the parts-and-assemblies approach was the natural choice since hardware failures were a major problem and the approach is an excellent technique for organizing maintenance. The machines were maintained by replacing assemblies and studying the failure modes of the parts and assemblies. This same maintenance technique is still in use today.
In the next chapter we shall discuss the problems of using the parts-and-assemblies concept in the construction of software. Also, under the assumption that many software systems being constructed today are similar, we shall outline a method for constructing software using parts and assemblies and advocate its use in the construction of similar systems.
The purpose of this dissertation is to apply the parts-and-assemblies concept to software construction. A software component is analogous to a part. From our discussion in Chapter 1, this means that a component can be viewed as either a part or an assembly depending on the level of abstraction of the view. A particular component usually changes from a part to an assembly of subparts as the level of abstraction is decreased. The duality of a component is a very important concept. The failure to deal with this dual view caused some problems with earlier work on reusable software.
The major problem with earlier work on reusable software is the representation of the software to be reused. In program libraries the programs to be reused are represented by an external reference name which can be resolved by a linkage editor. While a functional description of each program is usually given in a reference manual for the library, the documentation for a library program seldom gives the actual code or discusses the implementation decisions. The lack of this information prohibits a potential user of a library program from viewing it as anything other than a part. If the user can treat a library program as an isolated part in his developing system then the program library will be successful. Mathematical function libraries fit well into this context.
Usually, however, a user wishes to change or extend the function and implementation of a program to be reused. These modifications require a view of the program as an assembly of subparts and a part of many assemblies. To decrease the level of abstraction of a library program to view it as an assembly of subparts requires information about the theory of operation of the program and implementation decisions made in constructing the program. To increase the level of abstraction of a library program to view it as part of a collection of assemblies requires information about interconnections between programs in the library and implementation decisions defining common structures. None of this information is explicit in a simple program library. The burden is placed on the user of the library to extract this information.
The view of software components as isolated parts also plagued early work on reusable code modules [Corbin71, Corwin72]. The software components to be reused in this work are code modules hundreds of source lines long. With the code available a knowledgeable human user could form an abstraction of a given code module by examining it, but this is difficult work requiring vast amounts of knowledge from many domains. The problem of understanding a code module is exacerbated by the large size of the code modules. The large size is required to help a potential user of a reusable code module set organize a program using a small number of module names. If the average code size of a reusable code module is small, then there will be too many code module names for the user to organize. If the average code size is large, then the code modules will turn out to be too inflexible to be used in a wide range of systems without human examination and tailoring in each use. As with program libraries, the burden of organizing a specific program is placed on the user because even though the structure between the reusable code modules is more easily discerned than in program libraries, it is not completely explicit.
To avoid the problems encountered with program libraries and reusable code modules we will use the computer to handle a huge number of module names. Each name represents a small flexible software component described at a level of abstraction above programming language source code which will allow us to view the component as an assembly of subparts and a part of assemblies.
In general it seems that the key to reusable software is to reuse analysis and design; not code. In code, the structure of parts which make up the code has been removed and it is not divisible back into parts without extra knowledge. Thus, code can only be viewed as a part. The analysis and design representations of a program make the structure and definition of parts used in the program explicit. Thus, analysis and design is capable of representing both the part view and assembly view while code can only represent the part view. In this chapter a method will be presented which extends the reusable parts theme into all phases of the software lifecycle rather than just the coding phase.
It has been a common practice to name new computer languages after stars. Since the system described in this dissertation is a mechanism which manipulates special-purpose languages it seems only fitting to name it after a structure of stars, a galaxy. Draco, Latin for dragon, is a dwarf elliptical galaxy in our local group of galaxies which is dominated by the large spiral galaxies Milky Way and Andromeda. Draco is a small nearby companion of the Milky Way. At 1.2E+5 solar masses and 68 kiloparsecs from Earth its small size and close distance to home is well suited to the current system, Draco 1.0, which is a small prototype.
The Draco system addresses itself to the routine production of many systems which are similar to each other. The goal of this work is to be able to build large, understandable, maintainable, documented systems which represent an error-free implementation of the user's needs and desires. The particular approach the Draco system takes is the extension of the reusable parts-and-assemblies theme into the analysis and design phases of software construction.
Draco is an interactive system which enables a user to guide the refinement of a problem stated in a high-level, problem-domain-specific language into an efficient, low-level executable program. As the user guides the refinement of his problem he may make individual modeling and implementation choices or rely on tactics (which he defines) to give guidelines for semi-automatic refinement. Draco supplies mechanisms to enable the definition of problem domains as special-purpose, high-level languages and manipulate statements in these languages into an executable form. The notations of these languages are the notations of the problem domain. The user is not asked to learn a new, all-purpose language. When the user interacts with the system it uses the language of the domain. The user specifies his problem in terms of the objects and operations of the problem domain.
If an organization were interested in building many customized systems in a particular application area, say systems for aiding travel agents, they would go out to travel agent offices and study the activities of travel agents. A model of the general activity of being a travel agent would be formed and the objects and operations of the activities identified. At this point, the analyst of the domain of travel agent systems would decide which general activities of a travel agent are appropriate to be included in travel agent systems.
The decision of which activities to include and which to exclude is crucial and will limit the range of systems which can be built from the model later. If the model is too general it will be harder to specify a particular simple travel agent system. If the model is too narrow the model will not cover enough systems to make its construction worthwhile.
Once the analyst has decided on an appropriate model of travel agent activities, he specifies this model to the Draco system in terms of a special-purpose language specific to the domain of travel agents and their notations and actions.
The idea here is not to force all travel agents into the same mold by expecting them all to use the same system. If the model of the domain of travel agents is not general enough to cover the peculiarities which separate one travel agent's actions from another, then the model will fail.
The domain of travel agent systems is specified to Draco by giving its external-form syntax, guidelines for printing things in a pleasing manner (prettyprinter), simplifying relations between the objects and operations, and semantics in terms of other domains already known to Draco. Initially, Draco contains domains which represent conventional, executable computer languages.
Once the travel agent domain has been specified, systems analysts trying to describe a system for a particular travel agent may use the model language as a guide. The use of domain-specific language as a guide by a systems analyst is the reuse of analysis.
Once the specification of a particular travel agent system is cast in the high-level language specific to travel agent systems, Draco will allow the user to make modeling, representation, and control-flow choices for the objects and operations specific to the travel agent system at hand. The selection between implementation possibilities for a domain-specific language is the reuse of design.
Design choices refine the travel agent system into other modeling domains and the simplifying relations of these modeling domains may then be applied. At any one time in the refinement, the different parts of the developing program are usually modeled with many different modeling domains. The simplifying relations are source-to-source program transformations. The individual design choices have conditions on their usage and make assertions about the resulting program model if they are used. If the conditions and assertions ever come into conflict, then the refinement must be backed up to a point of no conflict. The use of strategies based on a formal model to aid in guiding the process of refinement is discussed in Chapter 6.
Eventually, the travel agent system is refined into an executable language and it is output by the system. Along with this final program is a refinement history of the choices made at each point in the refinement. This refinement history can explain every statement in the final program at different levels of abstraction all the way back to the original statement in the high-level travel agent domain. The refinement history is a top-down description of the final program. The process which produces this history is not a top-down process. The refinement history states which components were used in the construction of a particular system. If a component is found to be in error in one system, then the refinement histories of other systems may predict failures in those systems which used the faulty component.
The primary result of this work is the ability to build models of a class of systems and use these models to create member systems of the class in a reliable and timely way. New models are built upon old models to minimize the effort in creating a new model. The programs produced from these models are very efficient with the major optimizations done in the intermediate modeling languages.
A side-effect of this work is that it provides a mechanism for specifying computer science algorithms and representations in such a way that one need not know the implementation details of an algorithm or representation to use it.
To elaborate the brief discussion above, four major themes dominate the way Draco operates: the analysis of a complete problem area or domain (domain analysis), the formulation of a model of the domain into a special-purpose, high-level language (domain language), the use of software components to implement the domain languages, and the use of source-to-source program transformations to specialize the components for their use in a specific system.
The Draco mechanism is a general mechanism which can create (from human analysis) and manipulate (with human guidance) a library of domains. The domains are separate from the mechanism.
Domain analysis differs from systems analysis in that it is not concerned with the specific actions in a specific system. It is instead concerned with what actions and objects occur in all systems in an application area (problem domain). This may require the development of a general model of the objects in the domain, such as a model which can describe the layout of the documents used. Domain analysis describes a range of systems and is very expensive to perform. It is analogous to designing standard parts and standard assemblies for constructing objects and operations in a domain. Domain analysis requires a craftsman with experience in the problem domain.
A Draco domain captures an analysis of a problem domain. The objects in the domain language represent the objects in the domain and the operations in the domain language represent the actions in the domain. This approach follows earlier definitions of a problem domain:
"A model of the problem domain must be built and it must characterize the relevant relationships between entities in the problem domain and the actions in that domain." [Balzer73]It is our view that all languages used in computing capture the analysis of some problem domain. Many people bemoan the features of FORTRAN; but it is still a good language for doing collimated output of calculations, the type of computing high-energy physics has done for many years. This is not to say that FORTRAN is a good analysis of the domain of high-energy physics calculation, but it did find its niche [Wegner78b]. Domains are tailored to fit into a niche as defined by the uses in which man is interested in using computers.
Domain languages usually differ radically in form from standard general-purpose computer languages. Appendix III presents some examples of domain language statements. Most of the examples are tabular forms since these seem to be easy to read. A decision table, document format, and ANOVA table are all good examples of possible constructs for domain languages.
As discussed on page, software components are analogous to both parts and assemblies. A software component describes the semantics of an object or operation in a problem domain. There is a software component for each object and operation in every domain.
Once a software component has been used successfully in many systems, it is usually considered to be reliable. A software component's small size and knowledge about various implementations makes it flexible to use and produces a wide range of possible implementations of the final program. The top-down representation (refinement history) of a particular program is organized around the software components used to model the developing program.
The use of components, which is discussed in Chapter 4, does not always result in a program with a block structure chart in the form of a tree. Usually, as with programs written by human programmers, the block structure chart of the resulting program is a graph as shown in figure 36. An example component for a low-level executable domain language is shown in figure 27.
The source-to-source program transformations [Kibler78] used by Draco strip away the generality in the components. This makes general components practical. The transformations also smooth together components, removing inefficiencies in the modeling domain. This makes small components practical. Since single-function, general components are essential to the parts-and-assemblies approach, the transformations make component-built systems efficient and practical.
A transformation differs from an implementation of a component (a refinement) in that transformations are valid for all implementations of the objects and operations they manipulate. Refinements can make implementation decisions which are limitations on the possible refinements for other components of the domain. In general, transformations relate statements in one problem domain to that same problem domain, while components relate statements in one problem domain to statements in other problem domains. Some source-to-source program transformations for a low-level executable language are shown in figure 11.
This section presents an SADT(TM) model of the use of Draco to produce software. SADT (System
Analysis and Design Technique) is a registered trademark of
SofTech Inc. and has been successfully used to model both
software systems and social systems [Connor80, Ross77]. Its ability to
model both kinds of systems is important here since the
parts-and-assemblies concept on which Draco is based requires social
modeling to show how a craftsman gains enough experience to create a
problem domain for Draco's use. For those readers unfamiliar with SADT,
Appendix I presents a brief introduction to the technique.

The viewpoint or emphasis in the model is showing how the productivity of
the organization may be increased by reusing the analysis and design of
one system to construct another system. From our discussion in Chapter 1
this is only worth-while in problem areas where there is a demand for many
similar systems (A0C2). In particular we wish to show how an organization
might acquire the information to reuse analysis and design while it
produces systems in a conventional manner.
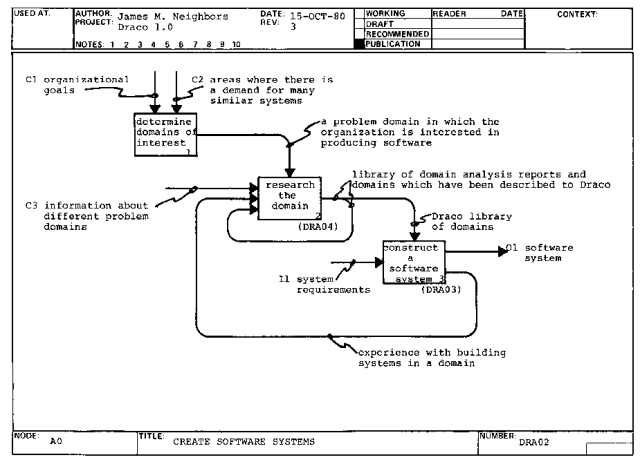
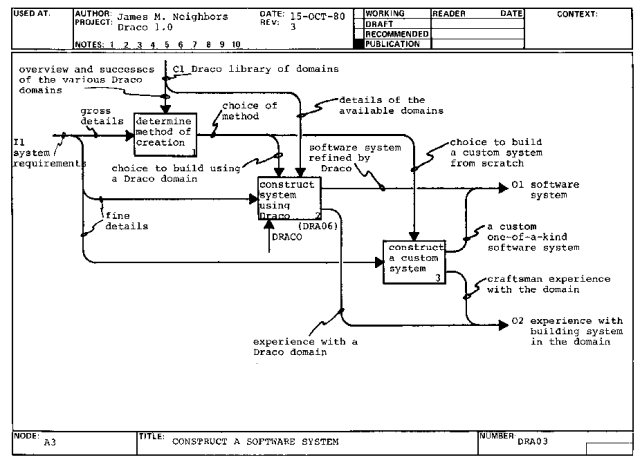
Meanwhile, the production arm of the organization accepts system
requirements for new systems (A0.3I1) and builds working software systems
(A0.3) either using Draco or a conventional method. The result of this
construction of software systems is either craftsman experience building a
custom system in some domain or experience with a Draco domain (A0.3O2).
This experience is used to help the organization establish or revise a
Draco domain (A0.2I2).
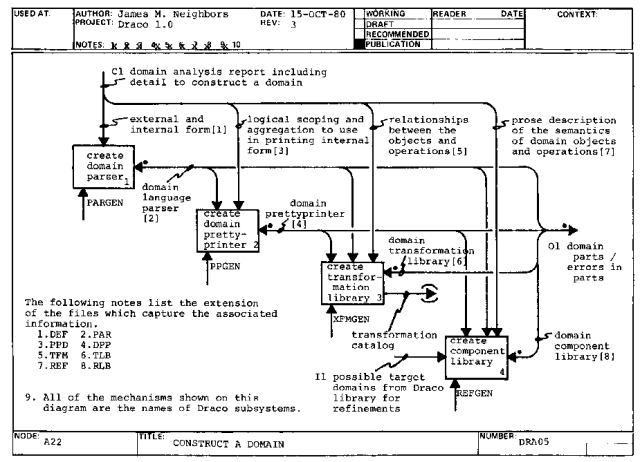
Next, a prettyprinter is created (A22.2) which can prettyprint the internal form of the domain back into the external form (domain language).
The third phase in the construction of a domain is the creation of a transformation library for the domain (A22.3) which is prettyprinted into a catalog of transformations for the domain.
The fourth and final phase in the construction of a domain is the creation of a component for each object and operation in the domain (A22.4). Each component contains many refinements which specify the meaning of the component in terms of other domains known to Draco (A22.4I1). As each refinement of a component is put into the domain component library, it is annotated with transformations of interest from the transformation library (A22.4I1) of the domain in which the refinement is written.
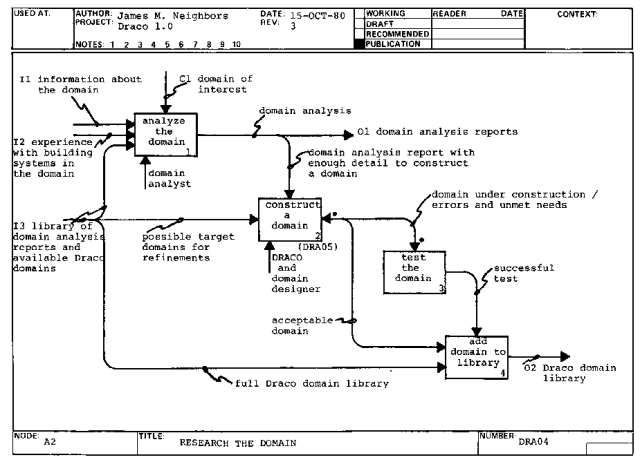
Feedback on problems with the definition of a domain is given through the
use of the domain (A22O1).
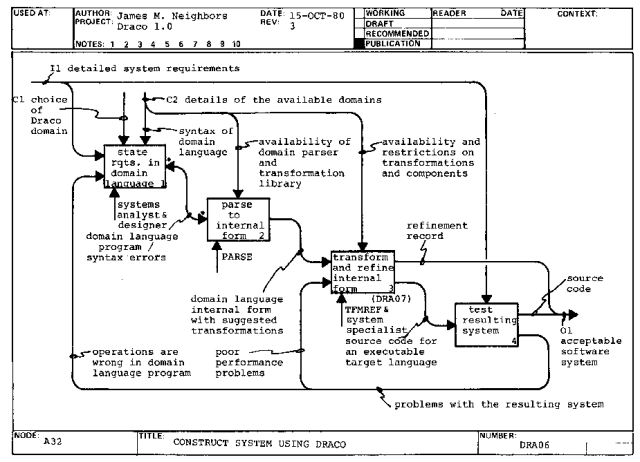
Once the program has been parsed into the domain internal form (A32.2O1), it is transformed and refined by a system specialist using the TFMREF subsystem into the source code of an executable target language (A32.3). The resulting software system is tested (A32.4) and is either acceptable (A32.4O1) or unacceptable. The refinement record (A32.3O1) of an acceptable system is retained.
The two types of unacceptable systems are those which seem to meet the
requirements but use too much resource (A32.3I2) or those which do not
meet their requirements (A32.1I2). An unacceptable system from a resource
standpoint may benefit from a new implementation. An unacceptable system
from a requirements standpoint requires revision of the domain language
program.
>
Once the problem has been refined into an executable language, the program (A323O2) is prettyprinted to a file.
From the previous model of the use of Draco in an organization to produce software, four major human roles with Draco are apparent.
From the model, we can see that the basic cycle of operation in producing an executable program with Draco is to cast the problem in a domain language, parse the domain language into the domain's internal form, optimize the internal form using transformations, refine the internal form using software components, and iterate transformation and refinement through layers of modeling domains.
The specification of the objects used in the Draco cycle of refinement is discussed in the next section.
A problem domain is a collection of objects and operations, but to specify a problem domain to Draco a few other things must be included. In particular, a domain language parser, a domain language prettyprinter, source-to-source transformations for the domain, and components for the domain must be specified to create a useable Draco domain.
A domain language parser takes the external form (syntax) of domain A, ext[A], and turns this into the internal form of domain A, int[A]. The domain language (the external form) should, if possible, use the notations and forms of the problem domain. The internal form of a domain is a tree with a prefix keyword in each node of the tree to state the purpose of that node. This is similar but not the same as a parse tree in that the prefix keywords are not nonterminal symbols in the grammar. All the manipulations of Draco are performed on this internal form.
In Draco 1.0 the syntax of the domain language is specified in a BNF style with tree-constructing operations included as actions. This scheme of parser description is taken from the META series of metacompilers [Schorre64]. The parser generator generates LL(1) class parsers from these descriptions.
A domain language prettyprinter takes int[A] and produces ext[A]. This activity is essential since Draco must communicate its actions and results in a form people can understand. The external form produced should be pleasing to the eye and produce useful groupings and indentations.
The details of specifying source-to-source transformations are dealt with in Chapter 3. The source-to-source transformations transform parts of the internal form of one domain into the internal form of that same domain, i.e., int[A] into int[A].
The transformations capture rules of exchange relating the objects and operations in the domain. These rules of exchange are independent of the implementations of the domain objects and operations. Each transformation is named and given a characterizing number which relates the importance of performing this transformation in the estimation of the domain designer.
The components for a domain relate the internal form of the domain to the internal form of other domain domains, i.e., int[A] to int[A,B,...,Z]. The details of specifying and using components are discussed in Chapter 4.
The components specify the semantics of the objects and operations in the domain. They do this by relating the objects and operations in one domain to the objects and operations in other (possibly the same) domains. There is a component for each object and operation in a domain. Each component contains many refinements each of which is a possible refinement for the object or operation in the domain which the component represents. Each refinement represents an implementation decision which may preclude the use of other refinements in other components. As an example, a string manipulation domain may support a string implementation as a singly-linked list of characters. This implementation would preclude a move string-pointer operation refinement which can back up in a string.
The details of domain specification may be found in the manual for Draco 1.0 [Neighbors80b]. In the following two chapters we will discuss the specification and use of transformations and components in more detail.
The source-to-source transformations used by Draco relate the objects and operations of a domain by specifying rules of exchange between statements in the domain. These rules of exchange are independent of any implementation decisions which may be made for the domain objects and operations.
Draco uses these transformations to customize the use of a component to its use in a specific system. Once a component is placed into a system, the transformations use the surrounding context information to smooth the component into the context and remove any unused generality.
Program transformations are productions with a left-hand side (LHS), a right-hand side (RHS), and enabling conditions [Standish76a]. The LHS is a pattern which is matched against the program. The enabling conditions are predicates on the parts of the program which are matched by the LHS. If the enabling conditions are true then the RHS is substituted for the LHS in the program. Since transformations are performed on a representation of the source code of a program, they represent optimizations independent of any particular machine.
By "source-to-source program transformations" we mean that the LHS is a pattern on the text, or source code, of the program and that the RHS is also a pattern of source code. In source-to-function transformations, the RHS is a function on the matched part of the program and the result of that function is substituted for the LHS.
In general, source-to-source transformations are not as expressively powerful as source-to-function transformations but their use is prompted by one important reason, the ability to understand what the transformations do. To understand a source-to-source transformation, the user must understand the language being transformed, the language of the transformation pattern matcher, and the language of the enabling conditions. The pattern language and the enabling condition language are usually very simple. To understand a source-to-function transformation, the user must further understand the language of the RHS function. This language is usually very complex and not at all the kind of thing a transformation user, who is concerned about the program and not about the transformation system, cares about learning.
In Draco, the source-to-source transformations should be intelligible to the domain builders, the domain users, and the Draco system specialists whose roles are defined on page. From now on we shall use transformations to denote Draco source-to-source transformations. Transformations are created by the domain builders. The simplicity of source-to-source transformations seems to increase their accuracy and make them more attractive to users.
Practically every transformation has enabling conditions if we wish to
insure strict semantic equivalence. Usually the full enabling conditions
are not checked. As an example the transformation
?X+0 => ?X
may have enabling conditions in that the "+" add operator may change the
type of ?X in some languages or normalize the representation of ?X in some
machines. By the same token the transformation,
(?B+?C)*?A <=> (?B*?A)+(?C*?A)
which requires the conventional enabling condition that ?A is side-effect
free [Standish76a], may alter the behavior of the program. All the
arithmetic operators on computers have side effects based on their range
of number representation. For any particular machine there are values for
?A, ?B, and ?C which can cause an arithmetic underflow or overflow on one
side of the transformation and not on the other. These kind of enabling
conditions are seldom checked since they would prevent most
transformations from operating and are not machine independent. In
general, the transformations are "probabilistic," checking for enabling
conditions which are usually violated. These include predicates on the
range and domain of variables in the program fragments under consideration
[Standish76a].
In Draco, transformations are specified as rules of exchange on the internal form of a domain language which is a tree with a keyword in each node to identify its function (prefix internal form). Thus, the LHS of a transformation is a statement in a prefix internal-form tree-pattern language.
Since the prefix internal form contains identifying keywords, a very fast, simple pattern matcher may be built using the keyword as a left-hand anchor in the matching. We can view the LHS as a tree template which is applied only to nodes in the internal form tree with the same prefix keyword as the root of the LHS pattern. Four types of objects may appear in the LHS pattern after the prefix keyword.
Metarules are rules which relate one rule to another rule. In the context of transformations as production rules, metarules relate the possible action of one transformation to the possible actions of other transformations [Kibler77]. Since the transformations used by Draco are source-to-source, we can automatically produce metarules for these transformations.
In the following discussion, LHS(t) and RHS(t) denote the right-hand and left-hand sides of transformation t, and a\b denotes whether pattern a matches pattern b. The details of the "\" metamatching operator are given in Appendix II. Metarules for a set of transformations, T, are created by the algorithm in figure 9. For each transformation t, algorithm 9 produces an UPLIST(t) and an AGENDA(t,n) for each node n in RHS(t).
ALGORITHM: Metarules(T)
INPUT: a set of transformations T
OUTPUT: for each t in T, priority queue UPLIST(t) and for each node n in RHS(t) priority queue AGENDA(t,n)
The UPLIST for a transformation t lists all the transformations whose LHS contains RHS(t). Thus if the transformation t were applied, the UPLIST(t) lists which transformations might apply at some internal form subtree which encloses the substituted RHS(t). The priority, DEPTH(n[j]), associated with each transformation given in UPLIST states where the transformation should be attempted as the number of tree levels above the node which was just transformed.
From steps 1 and 4 of algorithm 9, it is easy to see that the complexity of creating the metarules for n transformations is O(n^2) in terms of the "\" metamatching operator. Since this operator is expensive, and the number of transformations for a domain can easily range to 2000 [Standish76a], the transformations for a domain are grouped into a library and new transformations are incrementally added. The complexity of adding a new transformation to an existing library of n-1 transformations is O(n). All of the existing metarules still remain, just some new information is added to them.
As will be shown when we discuss the management of the transformations, the ability to generate metarules when the library is formed saves large amounts of searching when the individual transformations are used.
The designers of early transformation systems [ARSEC79] struggled with the problem of how to name each transformation in a large set of transformations so that the user could remember the names. The Draco system deals with this problem in two ways. First, the class feature in the definition of transformations allows one transformation to stand for many transformations depending on the size of the classes involved. Secondly, the metarules virtually eliminate the naming problem by having the transformations refer to each other by name. If a user knows where he wishes to perform a transformation then the metarules will have suggested only those transformations which could apply at that locale.
The number of names the user must recognize, not remember, is reduced to the transformations suggested for each locale. The metarule suggestions, coupled with the ability to display the text of a transformation from the catalog of transformations for each domain, eliminates the naming problem.
101 - up procedural transformations
not source-to-source
don't trace, don't ask user
11 - 12 always do this transformation
9 - 10 convert to canonical form
7 - 8 operator arrangement
5 - 6 flow statement arrangement
3 - 4 program segment arrangement
1 - 2 reverse canonical form
0 very seldom done, keys procedures
The application codes were designed for lookahead in the transformation process but this turned out to be largely unnecessary in the specialization of components discussed on page. They do turn out to be a convenient means for specifying actions to be taken by the transformation mechanism (i.e., convert to canonical form).
The example transformations in this section are on an ALGOL-like language rather than a domain language with which the reader would be totally unfamiliar.
5/3/79 19:18:18 SIMAL.TLB
<BOP> = {ASSIGN,EXP,DIV,IDIV,MPY,SUB,ADD,
NOTEQ,EQUAL,GTR,LESS,GTREQ,LESSEQ,AND,OR}
<REL> = {NOTEQ,EQUAL,GTR,LESS,GTREQ,LESSEQ}
<BOP>EMPX: 12 *EMPTY*<bop>?X => *UNDEFINED*
<BOP>IFELSEX: 4 (IF ?P THEN ?S1
ELSE ?S2)<bop>?X =>
(IF ?P THEN (?S1)<bop>?X
ELSE (?S2)<bop>?X)
<BOP>IFX: 4 (IF ?P THEN ?S1)<bop>?X =>
(IF ?P THEN (?S1)<bop>?X)
<REL>S0: 10 ?A-?B<rel>0 => ?A<rel>?B
ADDX0: 12 ?X+0 => ?X
EQUALMAMB: 12 -?A=-?B => ?A=?B
EXPX2: 9 ?X^2 => ?X*?X
FORXX: 11 FOR ?W:=?X STEP ?Y TO ?X DO
?Z => [[?W:=?X;
?Z]]
IFELSENOT: 12 IF ~?P THEN ?S1
ELSE ?S2 => IF ?P THEN ?S2
ELSE ?S1
LABELIFX: 10 ?X:
IF ?P THEN [[?S;
GOTO ?X]] =>
?X:
WHILE ?P DO ?S
MINUSSUBAB: 9 -(?A-?B) => (?B-?A)
PARPAR: 12 ((?X)) => (?X)
SEMICLXIF: 10 ?X:
?S;
IF ~?Y THEN GOTO ?X => ?X:
REPEAT ?S
UNTIL ?Y
When a domain language program is parsed into the domain's internal form, an agenda is established for each node in the internal form tree. If requested, the PARSE subsystem of Draco 1.0 will suggest transformations for each node in the program. Only transformations which will succeed in matching their LHS's are suggested by placing them in order of application code on the agenda of the node.
The transformation mechanism allows the application of transformations within a selected locale in an instance of a domain. Currently, the locale is selected by the user, but during optimization it really should be selected by analysis tools as discussed on page. The locale serves to focus the attention of the transformation mechanism to a small part of the program at a time. Within the locale the user may apply individual transformations to specific points in the program. The transformation suggestions on the agenda at any particular point in the internal form tree may be displayed by the user.
The individual application of transformations is a very tedious process. Alternatively, the user may request the transformation mechanism to apply transformations in the locale with some range of application code under some application policy with or without user approval of each transformation. Some transformation application policies and their meanings are given below.
As transformations are performed, the metarules for those transformations suggest other transformations. In particular, the RHS of a transformation already has agendas built into its tree form from the metarule creation. When a RHS is instantiated and substituted into the internal form tree, its agendas suggest transformations. Also, when a transformation is applied, its UPLIST is interpreted to add transformations on the agendas of nodes higher in the internal form tree than the node transformed.
Thus, the initial suggestion of transformations during parsing which could apply, coupled with the transformation mechanism's interpretation of the metarules, starts a chain-reaction which keeps all transformations which could apply to the program on the agendas of the internal form of the program. Since transformations are only put on an agenda if their LHS's match, LHS patterns are not attempted all over the program. This reduction in search in the application of a transformation to a locale makes the transformation mechanism very efficient in operation. This high efficiency will become important when "procedural" transformations are introduced in the next section.
With the use of metarules and the best-in-locale transformation application policy, some transformations which were previously considered procedural in nature may be implemented by a small set of source-to-source transformations in a comfortable way. These transformations introduce non-printing semantic markers into the internal form and rely on the metarules for their propagation through the internal form. The effect of the transformations and metarules is to create a Markov algorithm which runs on the body of the program being developed.
BEGIN LOCAL A;
.
.
GOTO LABEL1;
.
.
LABEL1: GOTO LABEL2;
.
.
IF predicate GOTO LABEL1;
.
.
END
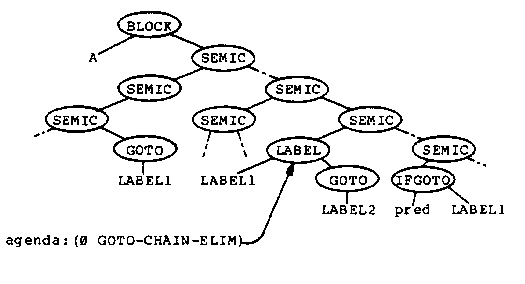
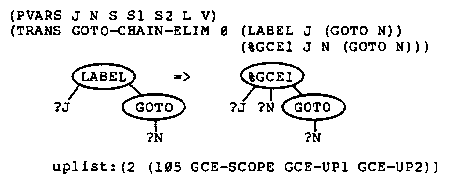
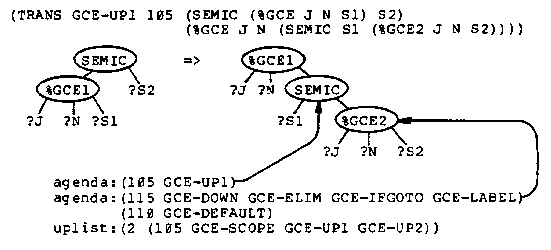
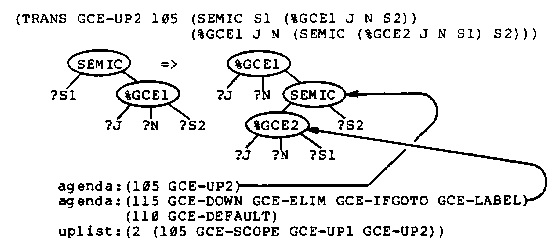
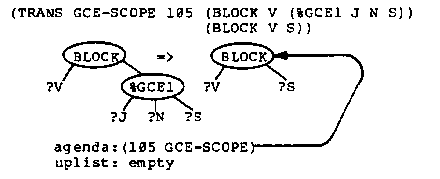
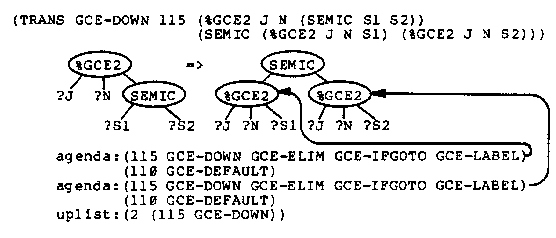
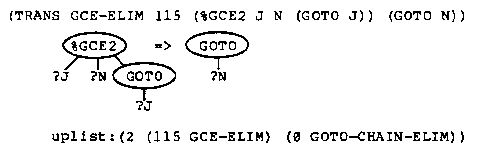
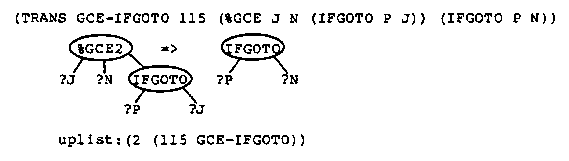
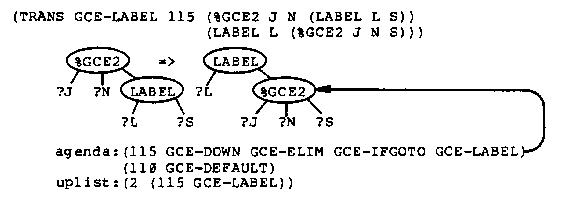
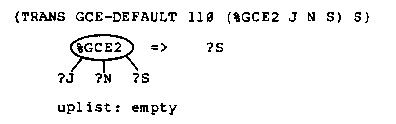
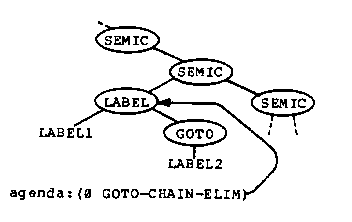
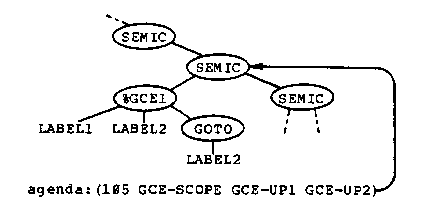
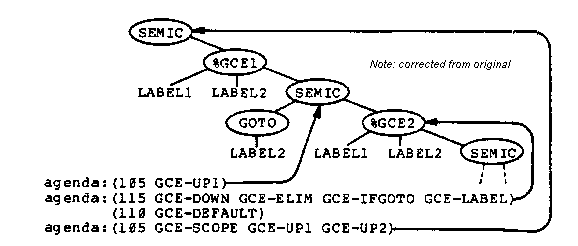
Because of the application codes, if there are %GCE2 markers in the tree then one of them is the locus of the next transformation. If there are no %GCE2 markers, then a %GCE1 marker moves up the tree and produces a new %GCE2 marker (GCE-UP1, GCE-UP2) or removes the %GCE1 marker when it encounters the scope of the label (GCE-SCOPE). At any time there is only one %GCE1 marker in the tree.
To avoid leaving semantic markers in the internal form, the transformations with application codes greater than 99 enlarge the locale if they are placed on an internal form agenda outside the locale. The resulting program is shown in figure 26.
BEGIN LOCAL A;
.
.
GOTO LABEL2;
.
.
GOTO LABEL2;
.
.
IF predicate GOTO LABEL2;
.
.
END
These procedural transformation sets are hard to understand and violate the ease of understanding motivation for source-to-source transformations, but they do serve to demonstrate a natural source-to-source technique for implementing some procedural transformations without having to learn an alien language capable of manipulating the internal form trees and writing RHS procedures.
Program transformation can be viewed as a game of perfect information, like chess. The program represents the current board position while the transformations which apply represent the legal moves. The goal of the transformation process is to achieve an optimal program under some criteria. Assuming we had an evaluation function on the program in terms of the criteria of optimization we could use lookahead with the evaluation function to suggest the next transformation to apply, much as the chess playing programs do today. The difficulty is in building the evaluation function which can determine the "goodness" of a given program under some general criteria. One approach to the evaluation function is to assign a "goodness" to each transformation. The application codes of transformations represents this approach. The increase in program "goodness" from applying a series of transformations is a function of the "goodness" of the individual transformations.
The ability to look ahead with Draco transformations is not very important since the transformations are used to specialize components. The degree of specialization could be improved by lookahead but the overwhelming majority of the work in specialization is in removing program fragments which represent unused generality. The relationship between components and transformations, discussed in Chapter 4, initiates transformation sequences to remove most unused generality without lookahead.
An alternative approach for transformation planning is to specify a goal in terms of the program and find some sequence of transformations which achieves the goal. This approach, currently under investigation by Fickas [Fickas80], avoids the huge search space of transformations encountered by lookahead, but it must deal with the problem of suggesting worth-while goals.
On page, the need to perform transformations on the correct level of abstraction is discussed. The transformations for a domain should only deal with the objects and operations of the domain and not anticipate or infer knowledge from other domains which map into or out of the domain.
In this chapter we have discussed how transformations are defined and used for specialization by Draco. The next chapter, which discusses software components, will investigate in detail the relationship between components and transformations. In particular, the theme of removing the responsibility for transformation suggestion will be carried over into components by automatically annotating the components with transformations to be considered.
Components provide the semantics for the domains specified to Draco. Each component represents possible implementations for an object or operation of a domain in terms of other domains known to Draco.
Each component must provide a semantics for the object or operation it represents which is consistent with the transformations of that object or operation in the domain. If, for example, a component represents the insertion of an element in a list, then the result of the operation should be a list. The internal actions of the list insertion component may break the input list structure into a structure which is not a list, but the result of the operation must be a list.
The concept of "granularity of meaning" is introduced here because earlier work in components attempted to prove that a component always upheld the structure of the object being manipulated. As an example, the properties of a list might be axiomatized and used in an attempt to show that a list insertion upheld all the axioms of a list. For most implementations of the insertion operation on a list, the axioms are not upheld since the insertion requires a temporary breakup of the structure of the list in a way which violates the axioms of a list.
In this work we assume that a well-defined component upholds the axioms of its input and output types only with respect to the external environment of the component (i.e., statements in the domain language in which the object or operation is defined).
An example component for exponentiation is shown in figure 27. The component provides the semantics for EXP internal form nodes for the language SIMAL which is not a domain-specific language, but will be used in examples so that the reader will not have to learn a domain-specific language at this point.
COMPONENT: EXP(A,B)
PURPOSE: exponentiation, raise A to the Bth power
IOSPEC: A a number, B a number / a number
DECISION:The binary shift method is O(ln2(B)) while
the Taylor expansion is an adjustable number
of terms. Note the different conditions for
each method.
REFINEMENT: binary shift method
CONDITIONS: B an integer greater than 0
BACKGROUND: see Knuth's Art of ... Vol. 2,
pg. 399, Algorithm A
INSTANTIATION: FUNCTION,INLINE
RESOURCES: none
CODE: SIMAL.BLOCK
[[ POWER:=B ; NUMBER:=A ; ANSWER:=1 ;
WHILE POWER>0 DO
[[ IF POWER.AND.1 # 0
THEN ANSWER:=ANSWER*NUMBER ;
POWER:=POWER//2 ;
NUMBER:=NUMBER*NUMBER ]] ;
RETURN ANSWER ]]
END REFINEMENT
REFINEMENT: Taylor expansion
CONDITIONS: A greater than 0
BACKGROUND: see VNR Math Encyclopedia, pg. 490
INSTANTIATION: FUNCTION,INLINE
ASSERTIONS: none
ADJUSTMENTS: TERMS[20] - number of terms,
error is approximately (B*ln(A))^TERMS/TERMS!
CODE: SIMAL.BLOCK
[[ SUM:=1 ; TOP:=B*LN(A) ; TERM:=1 ;
FOR I:=1 TO TERMS DO
[[ TERM:=(TOP/I)*TERM ;
SUM:=SUM+TERM ]] ;
RETURN SUM ]]
END REFINEMENT
END COMPONENT
A prose description of what the component does is given by the PURPOSE field. If the component takes objects as arguments and/or produces objects, then the type of these objects in terms of the objects in the domain is given in the IOSPEC field of the component. The DECISION field presents a prose description of the possible refinements of the component and the considerations involved in choosing between the alternatives.
Finally, there is a set of refinements of the component which represent a possible implementation of the component in terms of the objects and operations of other domains.
The first REFINEMENT in the set of refinements is the default refinement. In the absence of any other information, Draco will attempt to use this refinement first. Each REFINEMENT has a name and a BACKGROUND which is a prose description of the method the refinement implements and reference to where more information about the method may be found.
The CONDITIONS field of a refinement lists conditions which must be true before the component may be used. There are basically two kinds of conditions: conditions on the domain objects on which the component operates and conditions on previously made implementation decisions. The conditions on the domain objects are local to the locale where the component will be used. The conditions on the implementation decisions are global to the domain instance being refined. The ASSERTIONS field of a refinement makes assertions about the implementation decisions the component makes if it is used. The assertions are the opposites of the conditions on implementation decisions. The management of assertions and conditions is discussed in more detail on page.
The RESOURCES field of a refinement states what other components will be required to perform initialization if the refinement is chosen. The resource components are program parts which are executed before the resulting program begins execution (initialization phase) and they create information resources for the refinements used in the program.
An example use of a resource is a refinement for cosine which interpolates a table of cosines during execution. The table must be built during the initialization phase and the name of the table must be passed to the interpolation refinement of the component cosine. This is achieved by building a refinement which interpolates tables and requires a resource component which builds interpolation tables.
The ADJUSTMENTS field of a refinement states fine tuning settings for a refinement, the meaning of the adjustment, and a default setting. An example adjustment term might adjust the accuracy of a refinement or limit the amount of time spent in calculating in the refinement.
The GLOBAL field lists all names used in the refinement which are not to be renamed. The primary use of a GLOBAL definition is to define variable names which are reserved by a domain and cannot be renamed. The SNOBOL variable &ANCHOR is an example global. GLOBAL definitions should seldom be used and are always suspect. They seem to stem from a poor analysis of a domain. Labels which are defined in the refinement are defined in the LABELS field of the refinement.
The way a refinement may be inserted into the internal form tree during refinement is governed by the INSTANTIATION field of the refinement. The three modes of instantiation are INLINE, FUNCTION, and PARTIAL. More than one instantiation may be given for a refinement with the first one listed being the default instantiation. INLINE instantiation means the refinement is substituted directly into the internal form tree with all variables used in the refinement renamed (including labels) except for the arguments and those declared global. FUNCTION instantiation substitutes a call for the component in the internal form tree and defines a function using the refinement for the body. A new function is defined only if the same function from the same domain has not already been defined. PARTIAL instantiation substitutes a call for the component in the internal form tree with some of the arguments already evaluated in the body of the function defined. Limitations are placed on the partially evaluated forms allowed. When a function is defined the defining domain, component name, and a version number are used to differentiate between functions of the same name in different domains and FUNCTION and PARTIAL versions of the same function in the same domain.
The final field of a refinement is either a DIRECTIVE to Draco or the internal form of a domain. The internal form of a domain may be described either in a parenthesized tree notation with the INTERNAL:domain directive or it may be specified in the external form (domain language) of the domain with the CODE:domain.nonterminal directive. The CODE directive causes the parser for the specified domain to be read in and started to recognize the given nonterminal symbol. A DIRECTIVE to Draco is one of the following alternatives: view the component as a function definition by the user program, view the component as a function call, defer from refining this component, and remove the node which invoked this component from the internal form tree. The Draco DIRECTIVEs are used when a domain language is defined which allows function definitions, functions calls, and such things as refinements for comments which remove them from the program since they are saved in the refinement history.
Not all the component and refinement fields are required for each component definition. Basically the only required fields are COMPONENT, REFINEMENT, INSTANTIATION and CODE.
Components are placed into libraries in much the same way and for much the same reason that transformations are placed into libraries. The processing of a single component for inclusion in the component library of a domain is very expensive. For each refinement in the component, the parser for the domain(s) in which the refinement is written must be loaded to parse the external form into internal form. Once the code for the refinement is in internal form, the agendas of the internal form are annotated with transformations of interest from the transformation library of the target domain. These transformation suggestions are made in much the same way that transformation suggestions are made when a domain language program is parsed as discussed on page. The transformation suggestions will point out things of interest when the refinement is used. Thus, Draco supports a component library construction facility where a group of components may be replaced or added without disturbing the other components in the library.
This section discusses how the fields of a component are used in the refinement process to choose an implementation for the operation of object the component represents. Not all of these actions are accommodated in the current prototype system Draco 1.0. The differences between this narration and the prototype are given on page.
First the IOSPEC conditions on the component should be verified by examining the internal form or refinement history of the surrounding internal form of the node to be refined. Restrictions on the legal internal forms accepted by the domain language parser might make this step easier.
Next a REFINEMENT is chosen and the refinement CONDITIONS are checked. If an implementation decision condition is violated then the refinement may not be used. Local conditions on the domain objects are formed into surrounding code for the refinement body. The hope is that transformations for the domain will be able to remove this surrounding code by "proving" the conditions correct and removing the code.
The user is then asked about any ADJUSTMENTS for the refinement. If the user supplies no adjustments then the default adjustments are used.
The refinement body is now instantiated into the internal form according to the users wishes for INSTANTIATION and the allowed instantiations for the refinement. The body is instantiated with minimal renaming to avoid naming conflicts. If the refinement is instantiated as a function and a function already exists then the already defined function is used.
Once the refinement is inserted, any necessary RESOURCES are added to the initialization phase of the developing program. These resources are usually high-level program fragments which also have to be refined.
Finally the ASSERTIONS for the refinement are made in the scope of the domain instance. The assertions are a kind of lock and key mechanism with the conditions of other refinements. When two domain instances are merged into a single instance of a same or other domain, then the assertions are checked for consistency. This places the overly strong restriction that all objects in a domain of the same type have the same implementation. More experience with domains could probably remove this restriction. If the asserted conditions conflict, then the refinement of the program must be backed up. A model for avoiding conflicting assertions is given on page FORMALMODEL.
The model for the use of a component is very close to the actions of a module interconnection language (MIL). In fact it seems that a MIL is a natural way to organize the components of a particular domain. This similarity is discussed on page.
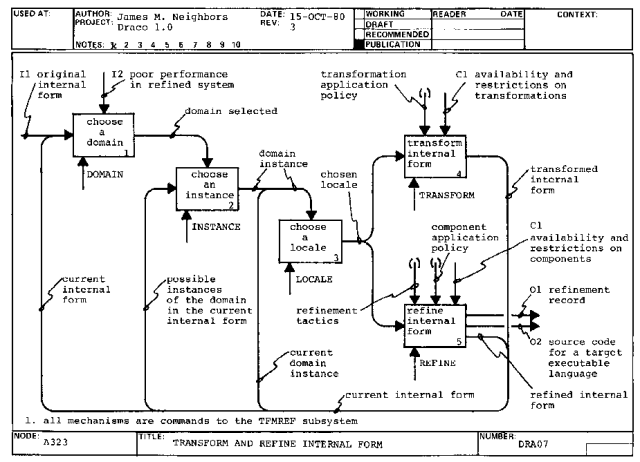
The refinement mechanism of Draco 1.0 applies the component library of a domain to a locale within an instance of the domain in the internal form tree for the program being refined. The locale is bounded by a domain instance which is a part of the internal form tree in the internal form of a particular domain. Refinements are made in one domain at a time on an instance of the domain. The locale mechanism is important for refinements in that the "inner loop" of the program should be refined first to pick efficient implementations. These implementation decisions will affect the choices outside of the inner loop through the assertion and condition mechanism of the components.
The Draco 1.0 refinement mechanism applies the components to the locale internal form tree using application policies similar to transformation application policies. In general, top-down application is the best policy to avoid conflicting conditions which would require a backup of the refinement.
From the previous discussion about the selection of a refinement for a component and the user interaction necessary to make a choice, it is evident that the user needs some mechanism to keep Draco from asking too many questions. The user needs the ability to specify guidelines for answering the questions and these guidelines are called "tactics."
The TACTICS subsystem of Draco 1.0 allows the user to interactively define tactics which answer refinement questions for the refinement mechanism. The subsystem also allows the user to read and write tactics from storage. A standard set of tactics is already available. When the refinement mechanism requires a user response, it first applies the tactics to see if one of them provides an answer.
DEFINE HEAD.*ENTRY* = COMPONENT,LOC 3;
DEFINE SPACE.*ENTRY*=[ALL<DIRECTIVE>,USE],
[ALL<AVAILABLE FUNCTION>,
USE FUNCTION],
[ALL<FUNCTION INSTANTIATION>,
USE FUNCTION],
USE DEFAULT;
DEFINE *CMD*.SUMMARY = "Summary:",COMPONENT,
PURPOSE,IOSPEC,DECISION,
[ALL,REFINEMENT,CONDITIONS,
BACKGROUND,ASSERTIONS,
RESOURCES,INSTANTIATION,
ADJUSTMENTS,DOMAIN];
EXIT
The SPACE rule checks all refinements to see if one is a Draco directive and if so, it uses it. Otherwise if there is a function which already implements the component, then the internal form node is replaced with a call to the function. Otherwise, if there is a refinement which can be instantiated as a function, then it attempts to use that refinement as a function. If all else fails, then it attempts to use the default refinement with the default instantiation. If none of the tactics is successful in producing a refinement, then the refinement user interface is invoked and the user may inquire as to the problem and make a refinement choice.
The *CMD* rules are rules which may be invoked by the refinement user interface. Thus, they are user-defined commands which may inquire about the state of the program under refinement and attempt to make refinement choices just as tactics would. The SUMMARY command prints out the fields of the component and all its refinements for the user's information and would be used if the user were required to specify a refinement.
The refinement user interface could be used for applying refinements one at a time but this would be very tedious work, similar to applying transformations one at a time. In general early versions of a high-level domain-specific program are refined by the default tactics, which use the usually easy and uncomplicated default refinements, to obtain a first implementation to see if the system implements the user's desires. Once a good domain-specific program is settled upon, the more sophisticated refinements and transformations may be used to refine the program for efficiency.
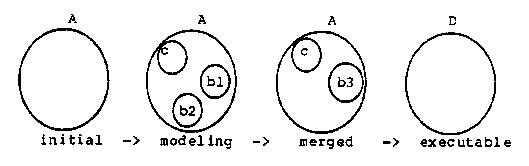
In Chapter 6, a formal model of the interdependencies of the domains which represent Draco's knowledge base is presented. Strategies based on this model should make it easier for a user to avoid knowing the details of the relationships between domains.
This chapter presents some results from using Draco in the construction of programs. To save the reader from having to understand a special-purpose domain language, the examples in this chapter are in the SIMAL language which is a simple infix Algol-like language. This language is not a domain language in the sense we have been discussing and is used here only for exposition purposes.
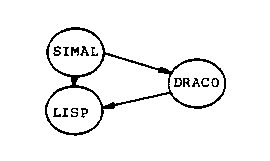
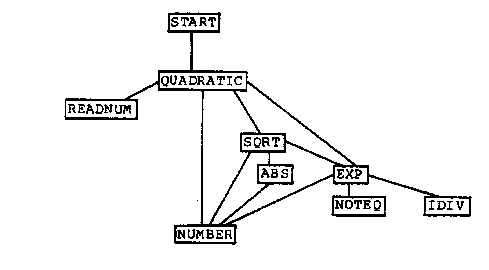
This chapter discusses an example which refines a quadratic equation solver from SIMAL into LISP. The three domains used in this refinement are organized as shown in figure 30. The DRACO domain shown in figure 30 creates functions, creates function calls, enforces component conditions, and eliminates scoping rules through renaming. It is the model of functions which Draco 1.0 uses.
In this section we will be discussing the refinement of the SIMAL program given in figure 32. The program represents a simple program for solving for the roots of a quadratic equation. The example is deceptively simple. The refinement of the SIMAL program into its equivalent LISP form must deal with the following problems:
.PROGRAM QUADRATIC
$QUADRATIC
[[ LOCAL A,B,C,ROOT1,ROOT2;
LOOP:
PRINT("QUADRATIC EQUATION SOLVER");
PRINT("INPUT A,B,C PARAMETERS ");
A:=READNUM;
IF A=0 THEN RETURN;
B:=READNUM;
C:=READNUM;
ROOT1:=(-B+SQRT(B^2-4*A*C))/(2*A);
ROOT2:=(-B-SQRT(B^2-4*A*C))/(2*A);
PRINT("THE ROOTS ARE: ",ROOT1," AND ",ROOT2);
GOTO LOOP ]]
$
.END
The first set of tactics used to refine the example are the "SS" tactics.
These direct the refinement mechanism to construct a function for each
component which can be made into a function. If a function for a component
already exists then a call to that function replaces the use of the
component. These tactics are designed to create "small and slow" programs
and are shown in figure 33.
DEFINE SS.*ENTRY* = LOC 2,
[ALL<DIRECTIVE>,USE],
[ALL<FUNCTION INSTANTIATION>,
USE FUNCTION],
[ALL<INLINE INSTANTIATION>,USE INLINE];
The second set of tactics used to refine the example are the "LF" tactics
which direct the refinement mechanism to instantiate a component inline if
possible. Otherwise the component is made into a function. The "LF"
tactics are designed to create "large and fast" programs and are shown in
figure 34.
DEFINE LF.*ENTRY* = LOC 2,
[ALL<DIRECTIVE>,USE],
[ALL<INLINE INSTANTIATION>,USE INLINE],
[ALL<FUNCTION INSTANTIATION>,
USE FUNCTION];
Both tactics are much simpler than is typically used in the refinement of programs. Tactics usually examine the assertions, conditions, possible instantiations, and target domain in their operation.
The second factor influencing the refinement of the example program was
whether or not the use of the transformation ?X^2 => ?X*?X was
allowed in the SIMAL domain. The transformation requires that ?X be
side-effect free [Standish76a]. If the transformation was allowed, it
was automatically suggested in all the components which could use it and
every time the transformation could be applied it was applied.
Table 1 names the programs produced under the circumstances outlined above. From table 1 we can see that the "SS" tactics met part of their objective in that the code space for the programs refined using them is smaller. The code size is the size of the static program for interpretive UCI LISP measured in 36-bit machine words. All measures of memory size are of this form.
transformation used
no yes
SS QUADSS QUADTSS
551 words 451 words
tactics 9 functions 6 functions
used
LF QUADLF QUADTLF
807 words 595 words
2 functions 2 functions
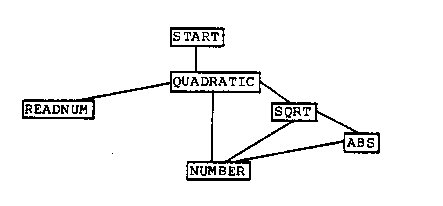
The block structure charts of the resulting programs is given in figures 36 through 35. The structure charts show that a single transformation can be very powerful in removing the need for the exponentiation routine and its support routines. The NUMBER routine shown in some of the structure charts arises from the need to maintain a consistent model of SIMAL numbers in LISP.
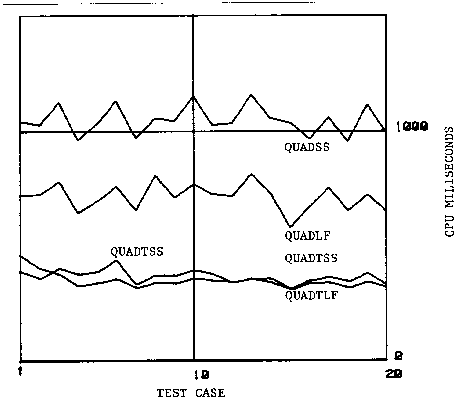
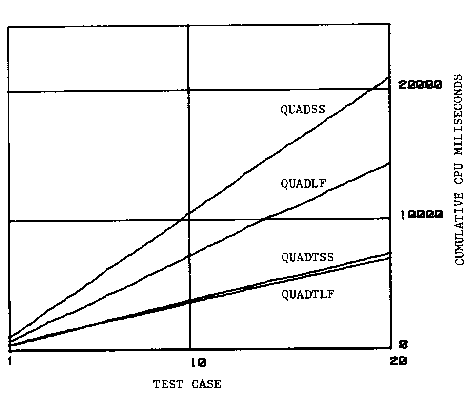
The runtime characteristics of the resulting programs was investigated by
running twenty test cases of the same random data through each program and
measuring CPU and memory use. Figure 38 gives the CPU usage of
all the programs for each test case while 39 gives the
cumulative CPU usage for each program as it ran the test cases.
Similarly, figures 40 and 41 give the memory use for
each test case and cumulative memory use for each test case respectively.
The variations in the amount of time and memory needed to run each test
case come from the SQRT and EXP routines which are iterative
approximations (Newton-Raphson and Binary Shift Method, see figure
27) and dependent on the input data.
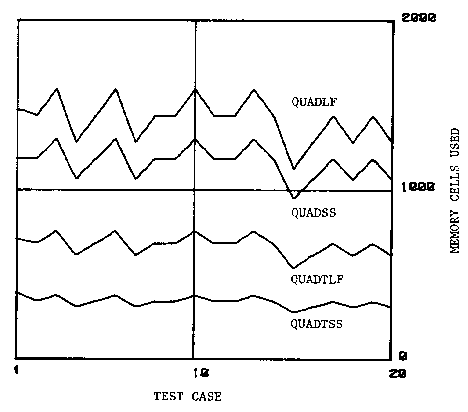
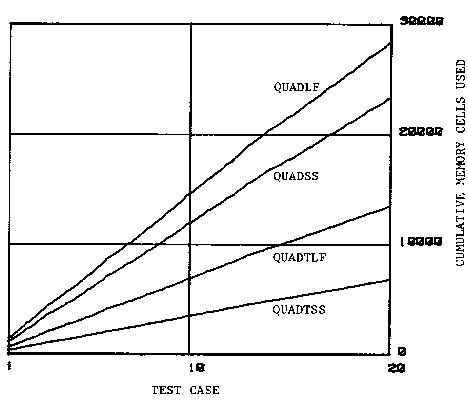
The runtime characteristics show that the programs refined with the "LF" tactics were larger and faster than their counterparts refined with the "SS" tactics. The difference in tactics, however, was completely dominated by whether or not the transformation was used. The programs which were transformed before refinement were faster and used less memory than those which were not transformed. This simple example demonstrates the importance of performing transformations at the correct level of abstraction as discussed on page.
Figure 39 shows that the QUADTLF implementation was just barely the fastest, beating QUADTSS, even though figure 40 shows that it requires twice as much running space as QUADTSS and its code space is larger. Without transformation, QUADLF is clearly faster than QUADSS and requires only about 20% more running space.
Which implementation is the "best" depends on the time-space tradeoffs in each specific case. The "LF" refined programs were presented at a disadvantage here in that the addition of more transformations would benefit them more since they are embeded inline and the transformations could make use of the surrounding context.
This chapter has presented a simple example which refined a 10 line Algol-like program into approximately 80 lines of LISP. This is clearly not the goal of this work, but it does serve to demonstrate some of the complex interactions which take place between the components, the tactics, and the transformations during refinement. The simple example did not even touch upon the issue of using alternate refinements for a component in that the given tactics always used the default refinement.
Only the ideas of transformations, components, and tactics are presented here. The details of the different definitions allowable in Draco 1.0 are found in the manual for the system [Neighbors80b].
The example in Appendix III uses many domains, more complex tactics, and large transformation libraries. There may be as many as 100 components for a domain each with two or three possible refinements. The transformation libraries may include 2000 or more transformations as the encoding of [Standish76a] for SIMAL does. The tactics may check many features in the context of refinement. The resulting programs may be 10-20 pages long. All of these facts make the transformation and refinement process a very complex operation. The next chapter introduces a formal model of this complex process which may serve as a basis for refinement strategies.
This chapter presents some models and ideas which arose from the use of Draco in the construction of programs. In particular, the nature of source-to-source program transformation, a formal model of the knowledge in Draco domains, and styles of domain organization are discussed.
Experience with source-to-source transformations as used by Draco has
shown that it is important to perform transformations at the appropriate
level of refinement. Continuing the example from Chapter 5, we can
consider the interaction between the SIMAL transformation EXPX2:
?X^2 => ?X*?X and the component for exponentiation shown in figure
27 which has two possible refinements, binary shift method and
Taylor expansion. Given an exponentiation in SIMAL there are three
options: use the transformation; use the binary shift method refinement;
or use the Taylor expansion refinement. For a specific case, of course,
fewer of the options may apply. The possible actions are shown in figure
42.
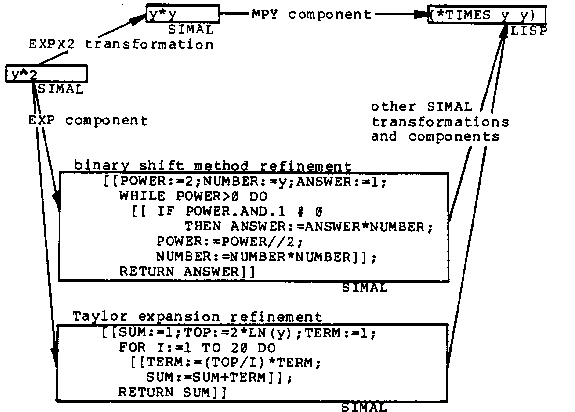
In the scenarios shown in figure 42 we are attempting to
refine the SIMAL fragment y^2 into a (*TIMES y y) in LISP. As shown, the
application of the EXPX2 transformation followed by the straightforward
refinement of a SIMAL multiply into LISP is the simplest approach.
The refinement of the exponentiation into the binary shift method makes the problem harder but still possible. The POWER could be propagated by transformation, the WHILE loop "unrolled," the AND functions solved, the ANSWER propagated through the unrolled loops, the dead variables eliminated, and the [[...]] block structure removed. Sophisticated and powerful transformations could reduce the binary shift method to a simple multiply.
The use of the Taylor expansion refinement makes the problem unsolvable by general transformations. Of course, a single transformation specific to this particular problem could be defined, and one always exists; but the number of specialized transformations which must exist to do even small problems makes this approach unreasonable. A set of general transformations cannot transform the Taylor expansion into the equivalent multiply because the expansion is an approximation of the multiply. If the transformations are equivalence preserving they shouldn't transform an approximation of a number into the number.
It is attractive to build some specialized knowledge into the system which can deal with problems like the approximation given above. The specialized knowledge would be used to recognize that a specific problem exists and be used to solve the problem. It is the author's opinion that this approach is misguided. The object of the refinement is an exponentiation, not an expansion. An expansion is an implementation detail. The role of knowledge sources in program understanding is discussed on page.
Optimizations of an object or operation must take place on that object or operation and not a refinement of it. This means that for programs constructed by Draco, optimization cannot be regarded as an "after the coding is done" operation. It should most definitely be regarded as an "after the specification is acceptable" operation.
The example of using a transformation at the right level of abstraction which was used here is very simple. The same problem, however, is encountered in more complex settings. As an example in the Augmented Transition Network (ATN) domain, there is a transformation set which removes unnecessary arcs from the transition network. A powerful general set of LISP transformations would have little chance of achieving the effect of this ATN transformation set on the LISP program which results from an ATN description. This is because the LISP transformations deal with LISP primitives and not the states and arcs of an ATN description with which the ATN transformations operate.
Two conditions can cause an optimization to remain undiscovered by source-to-source transformation at the wrong level of abstraction. First, the information necessary to perform the transformation could have been spread out by implementing refinements. Second, the transformations are attempted on an implementation (or model) of the original objects and operations which is not exactly equivalent to the original objects and operations.
To fully understand the capabilities of Draco we must build and reason with a formal model of the technique.
A major goal of the formal model developed in this section is to be able to answer the reusability questions [Freeman76a] outlined below.
The formal model is also of use in answering the deadlock question during refinement. A deadlock during refinement occurs when two refinement decisions, say the implementation of a data structure common to two separately refined program parts, are inconsistent. This means that the refinement of the program must be backed up to a point where the deadlock did not exist. The detection of this deadlock should be possible from the formal model. The deadlock problem is a subproblem of the reusability questions and would be useful during interactive sessions with Draco.
Finally, the formal model should serve as a basis for the development of refinement strategies. It is expected that for all but toy problems the complexity of answering the reusability or deadlock questions would be prohibitively expensive. The formal model can still serve as a planning space for refinement strategies whose goal is to produce a good program under certain criteria with minimal backup during refinement. The ability to look forward during refinement separates the refinement strategies from the refinement tactics described in Chapter 4.
The formal model of the knowledge in Draco is based on a Petri net [Peterson77, Peterson78]. Following the definition of Agerwala [Agerwala79], a Petri net is a bipartite, directed graph N=(T,P,A) where
T={t1,t2,...,tn} a set of transitions
P={p1,p2,...,pm} a set of places
The union of T and P represent the nodes of the graph N which are
connected by a set of directed arcs A. A marked Petri net C=(T,P,A,M)
further specifies a mapping M:P->I where the set I assigns the
number of tokens in each place in the net. In Petri net diagrams, places
are represented by circles, transitions by bars, and tokens by black dots.
Typically, places model conditions while transitions model actions.
Figure 43 performs mutual exclusion because initially there is only one token in p3. Both t1 and t2 are enabled but only one may fire since there is only one token in p3. The choice of which transition fires is completely arbitrary. Thus, after a single transition firing, either p1 contains a token or p2 contains a token but both cannot contain a token. The procedures modeled to be in execution by the existence of a token on p1 or p2 never run simultaneously; they are mutually excluded. This form of Petri net modeling has been used extensively in operating systems theory to model the use of resources.
The knowledge in the domains known to Draco can be viewed as a Petri net
where the places represent the components in the Draco domains. The
transitions represent the action of performing a refinement or a
transformation. The arcs which connect the places and transitions
represent the ability to perform a refinement or transformation. Figure
44 represents a part of the net which models the transformation
and refinements discussed in the example of Chapter 5.
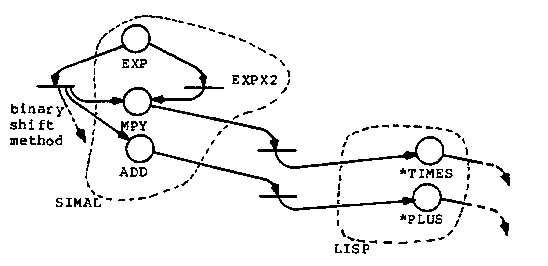
The dotted lines in figure 44 represent domain boundaries for the components of the two domains, SIMAL and LISP, involved in the example. Note that the transformation EXPX2 does not cross a domain boundary since it specifies a rule of exchange between statements in a single domain. Similarly, the transitions which represent individual refinement possibilities for a component always cross domain boundaries even if some or all of the resulting output places are in the same domain as the place of the component being refined. A refinement, of course, may refine a component into more than one domain at once.
The Petri net model discussed above provides a model of the
interconnections between components known to Draco through the
transformations and the different refinement alternatives for each
component. It does not model the information in a particular high-level
domain-specific program. The information specific to a particular problem
is modeled by a marking of the Petri net. For each node represented in the
internal form of the domain-specific high-level program a token is placed
on the Petri net representing the knowledge in Draco which represents that
node's semantics. The concept is illustrated in figure 45 for
the simple SIMAL statement X^2+5.
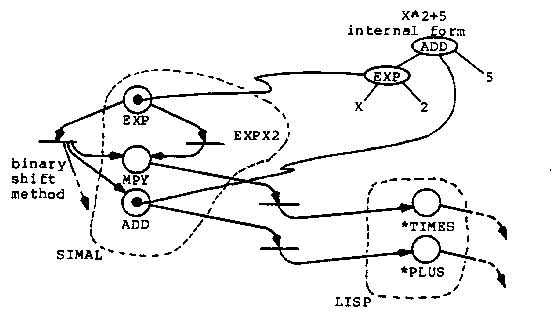
Each node in the internal form tree has a pointer to the token in the marked net which represents the use of a particular component. When a node is refined it uses the knowledge in the associated component. Tokens which represent nodes in other locations of the internal form tree are not disturbed. Only a transformation applied at a particular node may change the token representation of a subtree of the internal form. Refinements only refine a single node.
A formal definition of level of refinement and level of abstraction may be given with respect to the Petri net model of knowledge in Draco.
The level of refinement of a component in a specific problem is the number of refinement transitions which the token which represents that component has traversed since it was initially placed on the net.
The level of abstraction of a component in a specific problem with respect to a target domain is the minimum number of refinement transitions the token which represents that component must traverse in order to occupy a place in the target domain.
In this section we will show that the first two reusability questions and the refinement deadlock question are decidable, and thus can be answered. We will also show that the computational complexity of answering these questions for any practical case is extremely high. It is unknown if the third reusability question is decidable.
The discussion of this section will use a version of the formal model
which models only the use of components during refinement and ignores the
existence of transformations. Figure 46 presents a part of
the formal model which represents the existence of a refinement with
modeling conditions and modeling assertions.
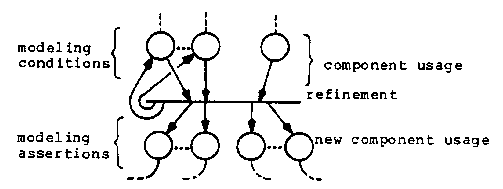
The places in figure 46 represent the existence of some condition, either the use of some component in the program under development or the assertion of some modeling condition. Thus, each possible modeling condition, like the use of singly-linked lists as a representation for strings, is modeled by the existence of a place in the formal model.
For a refinement to be used (i.e. the transition to fire) all the conditions must be indicated by the presence of a token and the component must be used in the developing program, indicated by the presence of a token in the component's place. When a refinement is used it places a token back on each of the condition places which enabled its use, indicating that each modeling decision is still in effect. Furthermore a token is placed on the places representing any modeling assertions made by the refinement. Of course tokens are also placed on the places representing the components used in the refinement.
To answer the reusability questions for a specific problem (Petri net
marking) with respect to a specific target domain some modification of the
net must be performed. First, the places which represent any modeling
decisions from all refinement assertions are individually connected
through a single-input, single-output transition to a newly defined place
we shall call the distinguished place. Second, all the places representing
the use of a component in the target domain are also connected to the
distinguished place through a single-input, single-output transition. The
distinguished place has the structure shown in figure 47.
Once we have modified the knowledge model net as described above, the first reusability question can be cast as the Petri net reachability problem. The reachability problem for Petri nets is as follows: given an initial marking of the net, is there a possible sequence of transitions which will produce a second specified marking of the net. The first reusability question is as follows: given the marking of the knowledge net model from some domain-specific, high-level program and a target domain, is there a sequence of transitions (refinements) such that only one token exists in the distinguished place and all other places are empty. The second reusability question is answered by the sequence of transitions specified to answer the first question.
The Petri net reachability problem has been shown to be decidable [Sacerdote77] and has been given lower bounds in time and space complexity [Lipton76]. Lipton has shown that the reachability problem will require at least an exponential (2^cn) amount of storage space and an exponential amount of time. The exponent (n) is the number of places and their interconnections to transitions. For the reusability questions, the number of places and interconnections is related to the number of components and modeling decisions and could give rise to exponents well over 100 for a single domain. The general reachability algorithm will not be practically applicable. The first two reusability questions are decidable, however.
Some hope still remains for an algorithm which can automatically refine a given domain-specific program in that general Petri nets may be a far too general model where a specific model of less power as discussed by Hack [Hack75] may have lower complexity bounds.
The inclusion of the general transformation mechanism discussed in chapter 3 into the formal model would render the reusability questions undecidable. The transformation mechanism allows the definition of Markov algorithms which are equivalent to Turing machines in computation power. Answering the reusability questions for an arbitrary set of transformations becomes equivalent to answering the halting problem for Turing machines, which is undecidable.
In describing the domains used in the examples of Chapter 5 it was useful to show the relationships between the domains using a directed graph as shown in figures 30 and 31. These graphs point out important considerations for someone interested in developing a set of domains to generate a particular kind of system.
Some domains, such as the TASK domain which provides parallel execution and the Draco domain which provides a model of functions, are domains close to computer science and exist mainly to be built upon. Other domains, such as the ATN domain, are more specialized and used as models by fewer domains. This suggests that one model of domain organization is to have a base domain which specifies a model of the resulting programs. All domains eventually map into this base domain. Computer science modeling domains surround this base domain supplying such things as data structures, control structures, and mathematical routines. On top of the modeling domains would rest the more application-oriented domains. One would expect the reuse of the components in a domain to increase the closer the domain is to the base domain.
There are several attractive candidates for the base domain including languages and computer architecture models. ADA, COBOL, LISP, and the UCSD Pascal P-machine are all languages which would be attractive base domains.
A model of machine architecture for a von Neumann machine is presented by Frazer [Frazer77a] in his work on code generators. Given an ISP description [Bell71] of a machine Frazer's system automatically builds a code generator for a simple von Neumann machine model dependent language for the described machine. The use of this language as the base domain could be one approach to the portability of high-level domain-specific programs between von Neumann machines. A model of a parallel dataflow machine is represented by the ID language [Arvind78]. In both cases, the description languages model the gross architecture of a particular class of machine. It is our contention that a program refined for a particular class of machine cannot simply be moved to a different class of machine.
The use of machine models as a base domain is a very old idea as demonstrated by the UNCOL project [Strong58] which attempted to build a universal computer-oriented language. The idea was that any program written in UNCOL could be automatically translated to any existing machine and take advantage of any special features of that machine. The UNCOL project failed because it attempted to form a model of the union of all features of all machines rather than their intersection. The motivation for this model was efficiency. In the end, UNCOL turned into a pattern recognition problem with patterns specific to a particular machine being used to recognize features of an UNCOL program which could take advantage of special target machine features.
The Draco approach to the UNCOL problem would have been to form a model of the intersection of the features of all machines in a specific class and use this as the base domain. The special features of a particular machine might only be used if they were directly stated as possible refinements in the modeling domains. A problem related to domain and knowledge organization is discussed in the next section.
The problem of translating a program in one general-purpose language into an equivalent program in another general-purpose language is related to the UNCOL problem. In terms of capability, of course, it can be done in that general-purpose languages are as powerful as Turing machines and a Turing machine can simulate any other Turing machine. A complete simulation of one language by another language is not a practical solution to the language translation problem.
To actually translate a program from one language to another and take advantage of the target language features, the translation mechanism must understand why each action exists in the original program.
This information is not in just the program code. To understand a simple program in a restricted domain would require many knowledge sources. The danger with research in automatic program understanding is that any particular example problem may be solved by specifying the appropriate knowledge sources. In general, however, the knowledge sources to understand an existing system are hard to construct. This paints a dismal view for anyone attempting to move systems which are only represented by source code, but the alternative is to build knowledge sources which would be very much larger than the source code.
The Draco approach to the language translation problem would be to save the refinement history for a particular program and re-refine a high-level description of the problem for a particular target language or machine model. The refinement history of a problem is very much larger than the resulting source code since it represents the interdependencies of the parts which make up the source code.
In terms of domain organization, programming language features should only be used in an appropriate domain. Special language features, such as SNOBOL string matching, are not appropriate to a domain which represents a model of general-purpose languages for von Neumann machines. However, SNOBOL string matching could be used as a model for matching in a string handling domain and SNOBOL primitives could be used as a possible refinement for the string matching components in the domain.
Most domains use more than one domain for modeling. The refinement process is not the strict translation of the entire program from one modeling domain to another until a suitable target domain is reached. Many refinements refine a component into two or three domains. At any one time, the developing program consists of program fragments in many modeling domains.
The organization of the domains is not a strict hierarchy; it is instead a cyclic directed graph. The implementation of arrays as lists and lists as arrays demonstrates a cycle. Another instance of a cycle is a cosine routine which interpolates a table which is built with a cosine routine. The cycles are not frivolous and many common representations rely upon them.
Finally, a problem domain is the same as a modeling domain to some degree. The ATN domain can be either a problem domain, if the problem is to build an ATN, or a modeling domain, if the problem is to build a natural language database which uses the ATN model of natural language parsing. As mentioned before, the closer in the domain organization a domain is to a base domain, the more likely its major use is as a modeling domain.
Two general trends seem to be apparent from the use of component parts by
Draco. Figure 48 presents the general increase of the number
of parts used with the development stage.
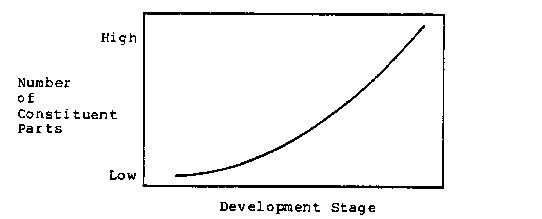
The curve in figure 48 is analogous to the number of tokens on the Petri net model of knowledge for Draco. If we assume that most component refinement alternatives are of about the same size, then the curve also represents the volume of the program in the measurement scheme of Halstead [Halstead77]. Relating Halstead's program volume by language level function to the Petri net model of knowledge in Draco could be an interesting topic of investigation.
Another trend in the use of component parts is shown in figure
49 which plots the average level of abstraction of the
constituent parts (defined on page) versus the
development stage.
The curve shown in figure 49 is analogous to the average path length of a token to the target domain. It must be remembered that cycles in the graph of domain organization can cause infinite path lengths and an infinite number of paths. Thus, figure 49 represents observed behavior in the examples as opposed to possible behavior.
If we combine the figures 48 and 49 we obtain an
estimate of the number of refinement decisions pending as shown in figure
50.
The number of refinement decisions pending at a given development stage is roughly the number of parts (figure 48) times the average level of abstraction of a part (figure 49). The increase in the modeling swell depicts the choice of possible modeling structures in many modeling domains for the developing program. The decrease in the modeling swell depicts the constraint of modeling choices already made. The modeling swell represents the largest barrier to refinement.
In Chapter 7 we shall discuss the origins of many of the ideas used by Draco and how the work on Draco might influence these ideas.
The inherent incompleteness of any survey of software production techniques is concisely stated in [Feldman72].
"Almost anything in computer science can be made relevant to the problem of helping to automate programming."An excellent overall discussion of the trends in software production research can be found in [Wegner79] which is outlined and motivated in [Wegner78a].
The organization of this survey forces recent work on software production into the categories of automatic programming, program generation, programming languages, software engineering, transformation systems, and philosophies of system structure. Each section is by no means a complete survey, but rather a representative sampling of current techniques. The discussion of each approach is very brief with references for the interested reader.
Automatic programming, which attempts to automate more of the system lifecycle than any other software production technique, can be divided into the knowledge-based approach and the formal-model-based approach. The knowledge-based approach relies on a knowledge representation scheme such as [Bobrow77] while the formal model approach uses a mathematical language such as predicate calculus.
These two approaches can be contrasted by comparing two works which synthesize sorting routines. The knowledge-based approach is characterized by [Green77] while [Darlington78] represents the formal model approach.
Knowledge-based automatic programming originated with experiments with compiling techniques [Simon63]. After a long dormancy, it was revived by work on robot planning such as [Sussman73] where the emphasis was on the knowledge in the system rather than the theorem proving which related it.
The Skill Acquisition From Experts system (SAFE) by Robert Balzer at USC/Information Sciences Institute [Balzer76a] accepts a problem specification in natural language. Through examination of the specification, rules about well-defined procedures, and question-answering, it attempts to discover the necessary facts to build a model of the problem domain [Balzer77, Balzer79, Wile77]. The model of the problem domain characterizes the relevant relationships and constraints between entities in the problem domain and the actions in that domain. Once the problem is in the form of a high-level procedure free of implementation details, it is refined using program transformations into an executable program [Balzer76b].
The PSI program synthesis system by Cordell Green at Stanford [Green76a] is a system of "cooperating experts" as described in [Lenat75, Hewitt73]. An expert system is a group of programs which communicate together to solve a problem. The PSI system consists of a trace expert [Phillips77], a program model building expert [McCune77], a domain expert, a discourse expert and user model, a coding expert [Barstow78, Barstow77a, Barstow77b], and an efficiency expert [Kant79, Kant77]. The program problem to be solved by the PSI system is specified in natural language and execution traces for a predefined problem domain as understood by the domain expert. The program model building expert interacts with the trace, domain, and discourse experts to extract the information to build a high-level procedure which is well-formed. The coding expert takes the well-formed (i.e., complete) high-level procedure and refines it to an executable program by proposing possible implementations to the efficiency expert and choosing an implementation based on the efficiency expert's analysis. The interaction between the coding expert and the efficiency expert has been closely studied in [Barstow76]. Knowledge about the problem domain in the PSI system is isolated in the domain expert. This means that, in theory, only the domain expert need be changed to apply the PSI system to a new problem domain.
The OWL system [Szolovits77] is a project whose aim is to accept the description of the problem domain in natural language and represent this domain knowledge as a network [Hawkinson75]. One motivation for this representation is that the system should be able to explain its actions in natural language. The natural language concept definition is still under development; but Protosystem I [Ruth76b], which takes in a complete high-level description of a problem in a domain and refines this into a program, has been completed. The input to Protosystem I is the operations to be performed, how often to perform them, on what data to perform them, and where the results of the operations are to be stored. The system analyzes the input, disambiguates the order of execution (sometimes by questioning the user), aggregates the data files on secondary storage, and, given the frequency of the different operations, generates the PL/1 and JCL necessary to create the system. The domain is restricted to business document processing.
An alternative refinement approach using the OWL knowledge representation is presented in [Long77]. This approach views all programs as a collection of a small number of model activities which are refined by stepwise refinement into an executable target language.
As will be discussed later in the section on programming languages, the reusability of a problem domain model to solve many problems in a domain will be a crucial problem in knowledge-based automatic programming.
Formal-model-based automatic programming started with work on deriving programs from proofs [Waldinger69a, Waldinger69b, Green69, Lee74]. The strict proof system approach was modified to use some knowledge-based reasoning [Buchanan74] in the construction of programs, but a formal model is still the driving force of this work.
The DEDALUS system by Zohar Manna and Richard Waldinger at Stanford [Manna77] synthesizes recursive programs and then translates them into iterative programs. The problem is specified in a formal language and operations on formal forms, usually sets and predicates on sets. The programming substitutions for each of the operations is pre-specified in a knowledge base. Using a goal system, DEDALUS expands its input specification by source-to-source transformation to try to achieve its output specification. If the system observes that the current subgoal, is an instance of a previous goal, then it forms a recursive procedure. The system can form mutually recursive procedures, recursive procedures with initialization procedures, and iterative procedures from recursive procedures. The recursive procedures it forms are checked for proper termination. The work of Burstall and Darlington [Burstall77], Wegbreit [Wegbreit76], and Follett [Follett78a, Follett78b] is similar to the DEDALUS system in approach.
J.R. Hobbs [Hobbs77b] describes a system for the translation of some of the algorithms specified in [Knuth68]. The knowledge about the primitives in the domain, in this case binary trees, is specified as predicate calculus equations related to English words. The system builds the program based on the structure of the English description. Different groups of English forms in the description are associated with different program forms. The system relies on the primitives of the domain to have been already defined as programs.
A final formal model approach under investigation is the synthesis of programs from input-output examples which is really aimed at solving subproblems in automatic programming. An example of the synthesis of programs form input-output pairs is found in [Shaw75, Biermann76]. This is related to the synthesis of programs from execution traces and simulated execution which were investigated in [Biggerstaff77, Cheatham77].
Many excellent surveys of the general field of automatic programming exist [Balzer72, Feldman72, Balzer73, Biermann76, Elschlager79]. A survey of the use of natural language in automatic programming is given in [Heidorn76].
Automatic programming systems have recently shifted from very powerful general problem solving techniques such as theorem proving [Waldinger69b] to knowledge-based systems with very little problem solving ability. Virtually all of the automatic programming systems under development today are knowledge-based rule systems, where the control mechanism is a production system and the rules are procedures, or patterns and procedures as described in [Davis75]. The shift away from general problem solvers should not be interpreted as the failure of general problem solving techniques to aid in software development. Rather, the investigation of these techniques has better defined the constraints on the problems which are best solved by general problem solvers.
Most of the automatic programming systems mentioned are still very much in the research phase of their development. The few operational systems are constrained to producing one to four page programs. In general, the design and coding phases of the systems are capable of producing large programs; but the specification and analysis phases are not.
Program generation work can be divided into two categories, model-based systems and parametric-based systems.
The model-based systems usually take statements in a special language as the specification. These statements are formed into a model of the program to be generated. Solution of a programming problem is attempted only if the input model is well formed under some model-building criteria.
Parametric-based systems could be called "programming by questionnaire" in that the user selects and restricts some features of a general system to create a system for his needs. An operating system SYSGEN procedure is the oldest example of this type of program generation.
It is hard to distinguish automatic programming systems from program generation systems. Both types of systems use many similar parts. In general, automatic programming systems interact with the user to acquire knowledge about the problem domain in order to write programs in that domain. Program generation systems do not really have a model of the problem domain as much as a model of a well-formed procedure. Usually the executable program is built directly from pre-existing source code parts.
The MOdule Description Language (MODEL) system of Noah Prywes [Prywes77a, Prywes79] from the University of Pennsylvania accepts the problem in a nonprocedural language where the order of the statements is irrelevant. Through data-flow analysis the statements are formed into a graph. The graph is checked for inconsistencies and ambiguities. Any problems with the specification are resolved by heuristics and user interaction. The well-formedness of the procedure represented by the graph is checked by examining the relationships between parent and successor nodes (program fragments) in the graph and checking certain rules on these relationships. An example rule might be "if a datum is produced, then some other part of the procedure should consume it." A clever matrix notation and matrix operations are used to perform these rule checks. From a well-formed graph the data files on secondary storage are aggregated for efficient access by the procedure. Finally the graph is directly translated into PL/1. The MODEL system operates in the domain of business data processing and is similar to Protosystem I [Ruth76b] in its input language and external operations.
Within the restricted domain of producing simulation programs for queueing problems having servers and things to be served, Heidorn [Heidorn74] describes a system which incrementally accepts a natural language description of the problem, checks the completeness of the description, produces a GPSS program to do the simulation, and produces a natural language description of the completed problem.
The AGE system [Nii79, Aiello79] is a program generation system with a model of what it means to describe a complete knowledge-based system. The system interacts with a user who selects knowledge-based system "chunks" which are parts used in the construction of the final system.
Similar to the AGE system is the Programmer's Apprentice project [Rich79] which attempts to generalize and modify a set of standard program plans under user direction to create a system. In this activity the programmer's apprentice is a knowledge-based system which performs the modifications and attempts to understand the construction goals of the programmer.
Parametric program generation trims and customizes a large model of a class of systems for a specific application. The parameters to the parametric program generation process remove unnecessary options of the general model and fill in some application-specific detail. The agent of program generation is usually a linking loader (linkage editor) or a conditional assembly scheme such as that used in assemblers. Most commercially available program generation systems are parametric program generators for a specific domain of application, such as business data processing.
"Parametric generation of programs is, by far, the most powerful technique known to date, if you measure power by the amount of information needed to specify a program in relation to the size of the program produced. If one wants to produce programs in a narrow envelop that are members of a closely related class, parametric generation is probably the best technique...Much of the automatic programming of the future will likely be done this way." [Standish75b]An example of program construction by questionnaire is given by Warren [Warren69].
A survey of the techniques of automatic program generation is given in [Prywes77b].
One technique is clearly not the final answer to the software crisis. The entire range of software generation techniques must be included in a program producing system.
"The people who work in this area (automatic programming) fully realize that for practical solutions, their ideas will have to be combined with those of the first type (program generation), incorporating specific knowledge of the domain being treated." [Feldman72]
Recent work in programming language design can be divided into the three areas of abstraction languages, extensible languages, and domain-specific languages.
Abstraction languages supply a mechanism for defining an abstract object and operations on that object while isolating the implementation details of the object and its operations. A new abstraction is built out of primitive types and previously defined abstractions. New abstractions are formed for each new application program, and abstraction libraries are advocated, but large-scale libraries have never been built.
The abstraction languages were motivated by the software engineering concept of hiding information in modules [Parnas72]. Early abstraction mechanisms were the SIMULA class concept [Birtwistle73] and Early's relational data structures [Early73]. Some examples of current abstraction languages are CLU [Liskov77], ALPHARD [Shaw77], and SMALLTALK [Goldberg76].
The abstraction concept has given a handle to program verification work in that abstraction can be verified and their formal semantics be used in verifying programs which use the abstraction [Flon79].
The goal of extensible languages is to start with a small set of primitive functions which will allow the extension of the language into a comfortable environment for the construction of an application program. The use of a small kernel of starting functions is advocated in [Newell71] and used extensively in many languages such as FORTH [Rather76] and LISP [McCarthy60]. Some of the problems with extensible languages had in meeting their goals are outlined by Standish [Standish75a].
An extensible language has been advocated as a medium of automatic programming [Cheatham72]. Usually the extensions of a language were redone for each application program, but recent work by Cheatham [Cheatham79] has advocated the reuse of extension alternatives as an aid in program production.
Domain-specific languages have objects and operations which model the objects and actions of a problem domain.
"It is a frequent misunderstanding that there is a separate category of languages called application-oriented. In reality, all languages are application-oriented, but some are for larger or smaller application areas than others. For example, FORTRAN is primarily useful for numeric scientific problems, whereas COBOL is best suited for business data processing." [Sammet76]It is the thesis of this work that a domain-specific language is actually an analysis of a class of problems in a specific problem domain.
An example domain-specific language is the Business Definition Language (BDL) [Hammer77, Howe75b] for the domain of business data processing. Quite a bit of effort went into the definition of this language, as shown by its constituent parts [Howe75a, Kruskal74a, Kruskal74b]. The BDL project also produced some tools for manipulating and using domain-specific languages [Kruskal76, Leavenworth76].
Many areas seem ripe for the development of a domain-specific language and possible objects and operations are discussed in many overview papers such as [Bullock78, Codd70, Woods70].
An active area in domain-specific language work has been in the languages suitable for describing software systems, specification languages, which are motivated in [Merten72] and described in [Teichrowe72]. Modern automatic programming systems usually model their programming problem and problem domain in a specification language [Goldman79]. The specification languages are not "executed" but "analyzed," as described in [Teichrowe76, Nunamaker76]. Blosser [Blosser76] describes the process of analysis and straightforward code generation from the design specification language given in [Teichrowe76]. These languages are used as models of a program to be derived.
The abstraction languages and extensible languages supply mechanisms for extending the language to suit the needs of a specific problem domain and encapsulating the implementation of domain objects and operations. The psychological set of this work is that it is easy to extend a language into a comfortable medium for discussing a particular problem in a problem domain. The author agrees with Standish [Standish75a] that this view is mistaken. It is the lesson of the developers of domain-specific languages and systems analysis techniques that the development of a good model of the objects and operations of a domain is only the result of long and intense analysis of the domain. As discussed in Chapter 2, a simple library of abstractions with strong abstraction definition schemes will not help very much with this problem.
Many of the techniques that Draco uses in constructing programs are directly related to software engineering research areas. In particular, the areas of module specification, module interconnection, software components, and program-feature analysis are of special interest.
Much of the work in software engineering has been concerned with how to build systems out of individual modules. The concept of modules is attractive because it represents a division of the work of producing a system into separate pieces which presumably can be built by separate people. Criteria to be considered in the division of a system into modules have been investigated by Parnas [Parnas72, Parnas78]. Basically, a module should perform only one function and hide the implementation details of how it performs its function. The concept is very similar to abstraction.
Once a system is divided into modules, module interconnection languages (MILs) are used to indicated how the modules fit together to form the system. This concept is advocated and most useful in the construction of very large systems [DeRemer76].
Typically a module interconnection language specifies the interfaces between modules by the type (abstract type), range and access allowed to the data being passed. Module interconnection languages have been advocated in many different settings [Campos77, Campos78, Goodenough74, Thomas76, Tichy79]. Primarily of interest here is the use of a module interconnection language to represent families of software systems as described in [Cooprider79, Tichy80]. This work used a MIL to coordinate the construction of similar software systems with different features for different target languages. The interconnection language that Draco uses for components is similar to these module connection languages.
The construction of software from components is a very old idea, perhaps known to Babbage. The recent interest in software components stems from their advocation by McIlroy [McIlroy69] at the 1968 NATO conference on software engineering. This same article also presents a panel discussion with arguments for and against the idea.
Some early work on software components [Corbin71, Corwin72] attempted to define general reusable components which were completely specified, fairly large programs of approximately 100 source lines. These systems strictly followed the hardware analogy of [Bell72] using port connections between components to create whole systems. In these experiments the components evolved to build a certain type of system were too specific to that class of system to be used in constructing other kinds of systems. Some later work [Levin73] managed to introduce some degree of flexibility by strictly following the module definition criteria of Parnas [Parnas72].
The work of Goodenough [Goodenough74] suggested that the smaller the component, the more flexible it is to use. Reducing the size of the components used by Draco (typically 5-10 source lines) and allowing components to be written in terms of other components has allowed the construction of general components flexible enough to apply to a large range of applications.
The management of software components and systems built with software components is discussed in [Edwards74, Edwards75]. An empirical study [Emery79] found that most of a system consists of the repeated usage of small software components.
The concept of software components used by Draco is modeled after the abstract strategies and program schema of [Standish73d, Standish74]. This same work also suggested the idea of having different strategies for the implementation of a component. The concepts and goals of reusability used by Draco were outlined in [Freeman76a].
By "analysis techniques" here we mean techniques for discovering properties about the developing program. These techniques would be useful to Draco in gathering information about the developing program which can be used to guide its further refinement. Some example techniques are module coupling and cohesion measures [Dickover76], incremental data-flow analysis [Babich78], program complexity measures [Halstead77], space and time use characteristics [Wegbreit75], and execution monitoring [Ingalls72].
The use of these techniques by Draco is discussed on page.
A collection of papers covering the major topics in software engineering is presented in [Freeman76b].
It is interesting to compare the program representations used by automatic programming, program generation, and software engineering. Most of the representations are data flow diagrams as described in [Ross76a, Ross76b]. This representation was investigated by Goldberg [Goldberg75] and was found to be a more natural specification of a procedure than the conventional control flow representation typically used in computer science.
A recent shift in software engineering has been towards integrated packages of tools for building large systems. These systems typically use special-purpose languages for describing the developing system, its environmental needs, and its current stage of development. Examples of such systems are ISDOS [Teichrowe76], the Software Factory [Bratman75], DREAM [Riddle78, Wilden79], Programmer's Workbench [Ivie77], the Unified Design Specification System [Biggerstaff79], and the Hughes design system [Willis79].
Program transformation systems manipulate a representation of the source code of a program. The mechanism used by most transformation systems is that of a production system [Davis75] where a single production represents a single transformation. Each production rule consists of a left-hand side (LHS) and a right-hand side (RHS). The LHS is matched against the program representation and, if found, is replaced by the RHS.
The work on transformation systems can be separated into those systems concerned primarily with optimization and those concerned primarily with the refinement of a program representation into an executable program.
Some early work on optimizing transformation systems stems from the desire to make the optimization process visible to the user [Schneck72]. These systems would like to perform the standard optimizations done by a compiler [Allen72] and exploit standard rules of exchange for the operators of general-purpose languages [Standish76a].
Recent interest in optimizing transformations was renewed by Loveman [Loveman77] in his attempt to define source-to-source transformations which group FORTRAN program features for execution on a parallel machine. Rutter [Rutter77] describes a source-to-source transformation system for LISP programs and examines the problems of controlling such a system. A transformation system designed to specialize a program on the basis of external knowledge about the data is described by Kibler [Kibler78].
Haraldsson [Haraldsson77] has investigated the use of partial evaluation of functions coupled with program transformations as a mechanism for optimizing programs. Partial evaluation is a process where all or some of the arguments to a function are instantiated in a special version of the function. These instantiations usually allow optimizing transformations to smooth the instantiations into their surrounding program context.
The use of source-to-source transformations in the conversion of programs back and forth from iterative and recursive methods is discussed by Darlington & Burstall [Darlington73], Arsec [Arsec79], and Manna & Waldinger [Manna77].
The possible use of metarules for transformation systems and an implementation scheme for transformation systems is discussed in [Kibler77].
Program transformations can be used for refinement if the LHS of a transformation is a statement in a higher-level language than the RHS of the transformation. In this way transformations can be used to fill in general plans of programs as shown in [Burstall77, Manna77, Wegbreit76, Ulrich79]. The plans range from recursive program schemes to loop generators for iterative programs.
The method of program synthesis from a tree and graph model of a program through tree transformations was investigated by Chesson [Chesson77]. This work discusses the kinds of operations useful in the manipulation and traversal of formally defined structures which represent programs.
The use of program transformation as a refinement mechanism useful in automatic programming has been suggested by Balzer, Goldman, and Wile [Balzer76b].
The correctness of program transformations is of great concern and a few techniques have arisen to verify the correctness of a transformation [Gerhardt75, Neighbors78]. The general power of transformation systems and their limitations was investigated by Kibler [Kibler78].
A criticism of the naive view of developing programs from a simple specification of the problem, as used in [Darlington78], and refining the simple specification into an efficient implementation is made by Dijkstra [Dijkstra77]. The criticism is made from the author's view that programs built on an underlying mathematical theory are not amenable to the transformation approach unless quite a bit of mathematical knowledge is supplied. This author would disagree that most programs are based on a mathematical theory, but we wholeheartedly agree that a transformation system must incorporate some domain-specific knowledge to be effective in transforming a program in a specific domain. Mathematics is but one of many possible domains in use today.
Many of the ideas that Draco incorporates have come from the philosophies of the researchers in software technology.
The use of domain-specific languages was motivated by software engineering and J.A. Feldman.
"There are many large groups of computer users who would be willing to use an artificial language if it met their needs." [Feldman72]
The use of abstraction, hierarchy, and components was influenced by Knuth [Knuth74], Standish, and Freeman [Freeman71].
"More generally, programming skills appear to consist of a rather rich inventory of methods applied at various times and at various levels of abstraction. These methods appear to span a cascade of knowledge systems from the problem domain to the programming domain, and to employ knowledge and representations from various appropriate modeling domains." [Standish73d]
The model of a domain description as a collection of objects and operations in the domain was influenced by Balzer.
"A model of the problem domain must be built and it must characterize the relevant relationships between entities in the problem and the actions in that domain." [Balzer73]
The concept of performing optimizations at the correct level of abstraction were motivated by Darlington and Ruth.
"We are able to make full use of the algebraic laws appropriate to this higher level. For example, once calls to set operations have been replaced by their list processing bodies many possibilities for rearrangement and optimization will have been lost." [Darlington73]
"Optimizations are most effectively performed at their corresponding level of translation, where exactly the sort of information and visibility needed is present." [Ruth76b]
The concept of keeping a refinement record for maintenance purposes was motivated by Knuth.
"The original program P should be retained along with the transformation specifications, so that it can be properly understood and maintained as time passes." [Knuth74]
The use of software components was motivated by Edwards [Edwards74], McIlroy [McIlroy69], and Waters.
"A pre-written module can be as simple as a multiplication routine or as complex as a data base management system. A module can be used as a subroutine or expanded inline as a macro. It can be partially evaluated or transformed after instantiation to increase efficiency. In any case, modules reduce the effort required to write a program because they can be used without having to be rewritten. They reduce the effort to verify a program because they can be used as lemmas in the verification without having to be reverified." [Waters76]
This section presents a summary of the results of the dissertation. Each point is discussed in more detail in the body of the dissertation.
The concept of domain analysis was introduced and compared to conventional systems analysis. Systems analysis states what is done for a specific problem in a domain while domain analysis states what can be done in a range of problems in a domain. Systems analysis describes a single system while domain analysis describes a class of systems. Since domain analysis describes a collection of possible systems, it is difficult to create a good domain analysis. If only one system is to be built, then classical systems analysis should be used. A domain analysis is only useful if many similar systems are to be built so that the cost of the domain analysis can be amortized over all the systems.
The key to reusable software is captured in domain analysis in that it stresses the reusability of analysis and design, not code.
The idea of a language as the medium for capturing a domain analysis was presented and it was hypothesized that languages in the past have really been the analysis of a domain of problems. This use of language as the medium for capturing a domain analysis is much different from the notion of extensible languages. A user trying to build a particular system does not extend the domain analysis; he contracts it for his particular problem.
A method was shown for producing variable implementations of a program through the use of reusable software components. These different implementations were equivalent in their actions and different in their structure and execution characteristics. The different implementations were optimized through the use of source-to-source transformations.
A scheme based upon Markov algorithms was presented for performing some "procedural" transformations without sacrificing all the advantages of source-to-source transformations. This scheme relies on the use of transformation metarules which relate transformations to one another. An algorithm for automatic metarule creation was presented.
A formal model of the knowledge in a set of problem domains which were defined in terms of each other was presented. A formal definition of the notions of level of refinement and level of abstraction were given in relationship to this Petri-net-based model. The question of whether or not the system has enough knowledge to refine a high-level description of a program to an executable program (the reusability questions) was discussed in terms of the model. In particular, the reusability questions are shown to be decidable and given a lower complexity bound.
The work succeeded in providing a context where the concepts of software components, module interconnection languages, and source-to-source program transformations work together to produce software. Previous to this work these concepts had existed as separate ideas.
The prototype system not only produces medium-sized efficient programs, but it can also be viewed as an educational tool. The components provide references to the computer science literature and present actual code for algorithms. To a small degree, the structure of the domains related to computer science relates the knowledge of computer science. A concept, such as random number generation, may be investigated by writing a program which uses random numbers and examining the knowledge sources the system uses to refine the program.
The concept of the system also might provide a framework for system analysis training in learning to discern the relevant objects and operations of a problem domain to construct a Draco domain.
Finally, the method of software production discussed presents an application oriented approach to technology transfer. If new algorithms are added to the system as they are developed, then the periodic remapping of existing systems from high-level, domain-dependent specification to executable program might be able to take advantage of some of the new information. The burden of importing the algorithm is removed from all the users and placed on the algorithm developer. This seems to be a stronger method of technology transfer.
The prototype system Draco 1.0 is available under the TOPS-10 operating system on the DEC PDP10 and its operational details are described in a manual [Neighbors80b]. Small programs may be created in 70K words of memory and the system has a 20-100 page program limitation since the developing program is not kept on secondary memory.
The prototype system helped to build itself in that all the input forms for parser descriptions, prettyprinter descriptions, component descriptions, and tactics are domain-specific high-level languages. While these descriptions don't go through the user directed refinement process as a user defined domain language would, they are processed by much the same mechanism. To change the form of these languages, their specifications are changed and remapped. Some semantic changes may be achieved the same way, while others may require a custom piece of code.
Much more work needs to be done on strategies for refinement which prevent the user from investing a large amount of time refining details which will have to be removed because the refinement deadlocks and must be backed up. This work should proceed along two lines.
One line of investigation deals with techniques for checking the validity of the refinement at a given point from the formal model of the knowledge in the system presented in Chapter 6.
The second line of investigation should deal with plans which are derived from the formal model. Because of the size and complexity of the formal model, the second line of investigation seems most promising in the development of strategies for refinement. The formal model may be viewed as a huge planning space which requires local heuristics for refinement. These heuristics would be refinement strategies.
Another area of investigation is the "unwinding" of decisions when backup in the refinement must occur. When backup occurs, it is because some knowledge is missing or some inconsistency appears in the implementation decisions. In theory, only the decisions which lead to the need to backup should be undone. The idea of minimal backup should be investigated, all the data for this process seems to be included in the refinement history. Along this same line, the reimplementation or modification of a system with few changes in implementation decisions should be able to take advantage of all the old decisions not changed or influenced. It seems important to develop a model of the interdependency of the decisions.
As they exist now, the assertions and conditions are a kind of lock and key mechanism. No effort is made to derive new information from either one. It would seem that the ability to establish relations for conditions and assertions would enable the refinement mechanism to deduce more information about the developing program. This work might directly influence the minimal backup and strategies work mentioned above.
The software production technique presented might be able to aid the work in software portability. The lowest level language known to Draco can be regarded as a model of the machine on which the resulting programs are to be run. This lowest level language would appear quite different for a von Neumann machine and a parallel machine, such as a dataflow machine. If the lowest level doesn't match the machine the program is to be executed on, then the use of that program is doomed to failure. A suitable level for the description of a machine's architecture can be found in the work on the automatic generation of code generators from a machine description [Frazer77a, Frazer77b]. In this work, a system which knows about the general architecture of a von Neumann machine (i.e., has a program counter, registers, and a memory) scans an ISP description of a particular machine to build a code generator for a specific machine for that language.
If the lowest level language known to Draco were one of these architecturally-oriented languages then it would seem that Draco coupled with a code generator generator and the ISP for a specific machine could produce code for that machine from a domain-specific high-level language to machine code. This is the goal of portability.
Virtually no work has been done on the handling of errors in the Draco system. The only work which applies is the protection of local conditions of interconnection which are turned into code and surround a component when it is used. The notation of error messages should be in terms of the problem domain in which the program was initially stated. Some of this information could be obtained from the refinement history but, in general, a notion of what each bit of code produced does in terms of the problem stated in the domain-specific high-level language needs to be carried along with the refinement process. Once refinement begins Draco currently has no notion of the domain in which the problem was originally stated other than the refinement history.
Draco incorporates no analysis techniques, such as data-flow analysis. Some analysis information can be obtained from special purpose "procedural" transformations, but this does not seem to be a good approach in that these transformation sets are expensive to run and hard to understand. Custom analysis tools would be better.
In general, different analysis techniques seem to exist for different levels of abstraction. As an example, execution monitoring, data-flow analysis, complexity measures, cost estimation techniques, and design quality metrics all apply to different levels of abstraction. Execution monitoring requires an executable program, while data-flow analysis requires a program with explicit data-flow, which excludes machine languages and non-procedural languages. The information from the analysis techniques pervades the program like the transformation suggestions (agendas) and the implementation decisions (assertions). The analysis information should in some way be incorporated into the internal form of the program.
If a domain analysis of analysis tools could be created it would be helpful in integrating the analysis information into the program internal form and for building new analysis tools for domain-specific languages at higher levels of abstraction.
Finally, much more domain analysis work is needed. This is very hard work which should only be attempted by a craftsman in a domain with some idea of the difficulty involved. It is an enlightening experience to try and define the objects and operations in a familiar problem domain. A good domain analysis requires many iterations of experiment and analysis.
Existing computer science knowledge needs to be formed into interlocking problem domains and this work is as hard as doing a domain analysis of a non-computer science domain. What are the objects and operations of data structures, compilers, parallel computation, or artificial intelligence problem solving? These domains have a lot written about them but their knowledge does not seem to exist in the form of a domain analysis. Very few domain analyses have been published in computer science, but when they are published, they usually are in the form of domain-specific high-level languages with specific objects and operations. An example of a domain analysis is the Business Definition Language (BDL) [Hammer77].
Perhaps the publishing of domain analyses has been slowed by the recent lack of interest in new programming languages. In the author's opinion, this lack of interest stems not from the new languages, but from the purpose of most of the new languages. Most of the new languages are general purpose-languages which contain no domain information from outside of computer science. The phrase "yet another ALGOL-like language" bemoans the definition of still more general-purpose languages. A research group which has done a domain analysis may be timid about publishing their results in the form of a language only to be met with the "another language" syndrome. A domain object in BDL is a document and it has a precise definition; this is not the same as the number, string, and list of general purpose languages.
Any tool, like Draco, which increases software productivity can be a blessing or a curse. The increase in productivity allows massive changes to be made in a large software system with relative ease. These changes must be seriously considered; not just from a technical viewpoint, but in the way they influence the users of the system [Scacchi80]. An increase in productivity should go hand in hand with stronger configuration management. Uncontrolled change in large software systems will lead to chaos regardless of the software tools used in the construction and maintenance of the systems.
In Chapter 2 an SADT actigram model of the Draco approach to software production is presented. SADT (System Analysis and Design Technique) has been used successfully to model both software systems and social systems. Its ability to model both types of systems is important here since Draco advocates the use of a software system within a social system.
A complete SADT model consists of two kinds of diagrams: activity diagrams (called actigrams) and data diagrams (called datagrams). The view of an actigram is that data objects flow between activities while the view of a datagram is that activities during their operation access data objects. The only difference is the center of attention. Only actigram models will be discussed in this appendix.
An actigram depicts three to six activities which are represented as boxes. The limit on the number of activities depicted helps to limit the amount of information a reader of an actigram must deal with. The boxes of an actigram are connected by arrows which represent data objects. Actigrams are data-flow diagrams. This means that the activity of a box takes place only when the data objects represented by incoming arrows to a box are present.
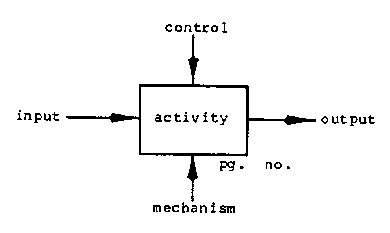
A double headed dotted arrow may be used as a shorthand in SADT to denote
data relations between activities as shown in figure 52.
Each actigram is an elaboration of an activity box in a higher-level diagram called the parent diagram. If a page number appears in parentheses just outside the lower right-hand corner of an activity box, then this number specifies the page of the actigram which elaborates the box. The inputs, outputs, controls, and mechanisms used in an actigram are the same as those on the corresponding activity box in the parent diagram. Each actigram should include from three to six activity boxes.
The highest-level actigram of a model is the only exception to the three to six activity rule and it presents only one activity, the one being modeled. The inputs, outputs, controls, and mechanisms which are used in the rest of the model are specified on this highest-level actigram called A-0. The A-0 actigram represents the context in which the system being modeled operates. As a part of the context the A-0 actigram explicitly states in prose the purpose of the model and from what viewpoint the model was made.
The external inputs, outputs, controls, and mechanisms used in an actigram are labeled with the position of the corresponding arrow on the corresponding box in the parent diagram. Inputs and outputs are numbered top to bottom while controls and mechanisms are numbered left to right. Thus, A2.3I2 (on actigram A2, box three, second arrow from top on left of box) would be shown as an external input labeled I2 on actigram A23. The numbering of the data objects with I ,C ,O , and M are called ICOM codes. If an external data object appears in an actigram and not on the corresponding box in the parent diagram then rather than being denoted by an ICOM code it is "tunneled." This means that the start or finish of the arrow is surrounded by parentheses to denote that the data object does not appear on the parent diagram.
The above discussion is a very brief introduction to SADT. More information about SADT can be found in [Connor80, Ross77, Ross76a, Ross76b].
There are three major stages in reading an SADT actigram model. At each stage the reader should ask the questions listed below.
Usually comments written on the diagrams are returned to the author of the model. The author then responds to these comments and returns them to the reader. This cycle of written comments between a reader and an author is called the author-reader cycle.
In figure 9 of Chapter 3 an algorithm for producing metarules for a set of transformations was given using the metamatching operator "\" which matches patterns against patterns. The metamatching algorithm is presented in detail in figure 53 of this appendix.
The four different types of objects which could appear in a Draco
source-to-source transformation pattern were defined in Chapter 3 on
page. They are literal objects, class variables, pattern
variables, and patterns.
ALGORITHM Metamatch(a,b)
INPUT: transformation tree patterns a and b
OUTPUT: boolean indicating whether a and b could match
The algorithm simulates the pattern matching of the transformation
mechanism. It matches two patterns without binding the pattern variables
to literal objects but to the minimal set of literal objects indicating
the restrictions on the match. As the matching proceeds more restrictions
are put on the possible values of the pattern and class variables. The
bindings of the two patterns share data so that if a restriction of a
pattern or class variable occurs during its use in the pattern, then this
restriction also applies to everything which has matched that variable in
the past. If a new restriction is inconsistent with the previous use of
the variable, then the match fails. As an example, the transformation
pattern
IF ?w THEN ?x
with internal form
IF ?a THEN ?b+?c ELSE ?d-?c
with internal form
type of b[ij]
literal class pattern pattern
object variable variable
literal do do do match
object step 2 step 4 step 4 fail
type class do do do match
of variable step 4 step 4 step 4 fail
a[ij]
pattern do do do do
variable step 4 step 4 step 4 step 4
pattern match match do do
fail fail step 4 step 3
type of b[bind]
no literal set pattern
binding object
no do do do do
binding step 5 step 6 step 7 step 8
type literal do do do match
of object step 6 step 9 step 10 fail
a[bind]
set do do do match
step 7 step 10 step 11 fail
pattern do match match do
step 8 fail fail step 12
This appendix presents two example domain language programs and samples of their execution. The first example implements a natural language parser and natural language generator for a restricted domain of discourse. The second example uses the same domain used to construct the parser of the first example to couple a natural language parser to a relational database. All of the examples shown here are actual input to Draco 1.0 and were refined by the prototype system.
This section demonstrates example domain-specific languages for specifying natural language parsers and generators for a restricted domain of discourse. The example consists of three parts: a dictionary, an augmented transition network (ATN), and a generator. The specific ATN used in the example was originally specified by Woods [Woods70].
The dictionary specifies the allowable words, their part of speech (class), and special word features. A particular word may be a member of more than one class (such as "was") and as a class member have more than one interpretation or feature list. An example dictionary is shown below.
DICTIONARY DWOODS
; Dictionary for the examples in Woods and Burton
; Abbreviations
; NP = noun phrase NPR = nomitive pronoun
; PPRT = past participle ADJ = adjective
; ITRANS = intransitive AGNTFLG = agent possible
; TRANS = transitive DET = determiner
; PREP = preposition S-TRANS = sentence object
; PRO = pronoun AUXVERB = auxiliary verb
;
; word | class | features
;-----------------------------------------------------------
John | NPR |
was | VERB | ROOT:be TENSE:PAST
|AUXVERB| ROOT:be TENSE:PAST
believed| VERB | ROOT:believe PPRT TENSE:PAST
to | PREP |
have | VERB | ROOT:have UNTENSED TRANS
been | VERB | ROOT:be PPRT
shot | VERB | ROOT:shoot TENSE:PAST PPRT
by | PREP |
Harry | NPR |
; the following words are root word entries
believe | VERB | TRANS ITRANS S-TRANS
ROOT:believe PPRT:believed PAST:believed
be | VERB | ITRANS ROOT:be PAST:was
shoot | VERB | TRANS ROOT:shoot PPRT:shot PAST:shot
.END
The particular natural language parsing scheme used in the example is an augmented transition network (ATN) [Woods70, Burton76]. The ATN states how the words in the dictionary may be combined into well-formed sentences. The input to an ATN is a dictionary and a sentence. The output of an ATN is a set of syntax trees. If the sentence is ambiguous with respect to the dictionary and the ATN then the set of syntax trees contains all interpretations.
An ATN is based on a finite state machine with conditions and action augmentations on the arcs. In the example ATN given below the state names (such as SENTENCE and Q1) appear against the left margin. The example shows two arcs emanating from the SENTENCE state, one to state Q1 which advances the input to the next word and one to state Q2.
An arc may be traversed only after the tests on the arc have been passed and the actions on the arc performed. Thus, in the example the arc from SENTENCE to Q1 may only be traversed if the current word is an AUXVERB and the given actions have been performed. As mentioned before, the details of ATNs are given in [Woods70]. The parallelism inherent in finding all parses is implicit in the ATN description.
ATN WOODS
NETWORK SENTENCE
; see example in both Woods and Burton
; Abbreviations
; NP = noun phrase NPR = nomitive pronoun
; PPRT = past participle ADJ = adjective
; ITRANS = intransitive AGNTFLG = agent possible
; TRANS = transitive DET = determiner
; PREP = preposition S-TRANS = sentence object
; PRO = pronoun AUXVERB = auxiliary verb
;
;from to | tests | actions
;-----------------------------------------------------------
SENTENCE
+Q1 | class AUXVERB? | VERB:=word[ROOT]
| | TENSE:=word[TENSE]
| | TYPE:='QUESTION
; ------------------------------------------------------
Q2 | none | SUBJ<=NOUN-PHRASE
| | TYPE:='DECLARE
;-----------------------------------------------------------
Q1 Q3 | none | SUBJ<=NOUN-PHRASE
;-----------------------------------------------------------
Q2 +Q3 | class VERB? | VERB:=word[ROOT]
| | TENSE:=word[TENSE]
;-----------------------------------------------------------
Q3 +Q3 | class VERB? | put SUBJ on hold as NP
| is word PPRT ? | SUBJ:=('NP
('PRO 'someone))
| VERB='be | AGNTFLG:='TRUE
| | VERB:=word[ROOT]
; ------------------------------------------------------
+Q3 | class VERB? | TENSE:=TENSE+'PERFECT
| is word PPRT ? | VERB:=word[ROOT]
| VERB='have |
; ------------------------------------------------------
Q4 | is VERB TRANS ? | OBJ<=NOUN-PHRASE
; ------------------------------------------------------
Q4 | holding NP? |OBJ::=remove NP from hold
| is VERB TRANS ? |
; ------------------------------------------------------
exit | is VERB ITRANS ? | <=('S ('TYPE TYPE)
('SUBJ SUBJ)
('VP ('TNS TENSE)
('V VERB)))
;-----------------------------------------------------------
Q4 +Q7 | word='by | AGNTFLG:='FALSE
| AGNTFLG='TRUE |
; ------------------------------------------------------
+Q5 | word='to | none
| is VERB S-TRANS ? |
; ------------------------------------------------------
exit | none | <=('S ('TYPE TYPE)
('SUBJ SUBJ)
('VP ('TNS TENSE)
('V VERB)
('OBJ OBJ)))
;-----------------------------------------------------------
Q5 Q6 | none | SUBJ|:=OBJ
| | TENSE|:=TENSE
| | TEMP:='DECLARE
| | TYPE|:=TEMP
| | OBJ<=VERB-PHRASE
;-----------------------------------------------------------
Q6 +Q7 | word='by | AGNTFLG:='FALSE
| AGNTFLG='TRUE |
; ------------------------------------------------------
exit | none | <=('S ('TYPE TYPE)
('SUBJ SUBJ)
('VP ('TNS TENSE)
('V VERB)
('OBJ OBJ)))
;-----------------------------------------------------------
Q7 Q6 | none | SUBJ<=NOUN-PHRASE
;-----------------------------------------------------------
VERB-PHRASE
+Q3 | class VERB? | VERB:=word[ROOT]
| is word UNTENSED ? |
;-----------------------------------------------------------
NOUN-PHRASE
+NP1 | class DET? | DET:=word[ROOT]
| none |
; ------------------------------------------------------
+NP3 | class NPR? | NPR:=word
;-----------------------------------------------------------
NP1 +NP1 | class ADJ? | ADJS:=#ADJS+word[ROOT]
; ------------------------------------------------------
+NP2 | class NOUN? | NOUN:=word[ROOT]
;-----------------------------------------------------------
NP2 exit | none | <=('NP ('DET DET)
('ADJ #ADJS)
('NOUN NOUN))
;-----------------------------------------------------------
NP3 exit | none | <=('NP ('NPR NPR))
;-----------------------------------------------------------
.END
The natural language generator for the example shown below is also based on a finite state machine. The generator performs the inverse function of the ATN by taking in a syntax tree and a dictionary to produce a sentence.
GENERATOR GWOODS
NETWORK STREE
; This is the generator for the examples in Woods and Burton
;from to | tests | actions
;-----------------------------------------------------------
STREE S1 | none | gen SUBJ at SUBJECT
| | gen VP at VERB-PHRASE
;-----------------------------------------------------------
S1 exit| TYPE='QUESTION | out "?"
; ----------------------------------------------------
exit| TYPE='DECLARE | out "."
;-----------------------------------------------------------
SUBJECT exit| none | gen NP at NOUN-PHRASE
;-----------------------------------------------------------
NOUN-PHRASE
exit| PRO? | out PRO
; ----------------------------------------------------
exit| NPR? | out NPR
; ----------------------------------------------------
exit| DET? | out DET
| | list ADJS
| | out NOUN
;-----------------------------------------------------------
VERB-PHRASE
VP1 | TNS='PAST+'PERFECT| out "had"
| | out V[PPRT]
; ----------------------------------------------------
VP1 | TNS='PAST | out V[PAST]
;-----------------------------------------------------------
VP1 exit| OBJ? | gen OBJ at OBJECT
;-----------------------------------------------------------
OBJECT exit| NP? | gen NP at NOUN-PHRASE
; ----------------------------------------------------
exit| S? | gen S at OBJ-CLAUSE
;-----------------------------------------------------------
OBJ-CLAUSE
exit| none | out "that"
| | gen SUBJ at SUBJECT
| | gen VP at VERB-PHRASE
;-----------------------------------------------------------
.END
The example executions of the parser-generator pair are shown below. The testing program reads in a sentence, passes it to the ATN, and passes each syntax tree in the resulting set to the generator. The "*" prompt marks the input sentence which is followed immediately by the generator output and the syntax tree which produced the generator output. As far as the example is concerned, the input and generated sentences are equivalent. Only one of the sentences shown is ambiguous.
[DSKLOG started: 5-20-80 3:25 AM]
*(TESTER)
*was John shot
someone shot John?
(S (TYPE QUESTION)
(SUBJ (NP (PRO someone)))
(VP (TNS PAST) (V shoot) (OBJ (NP (NPR John)))))
*John shot Harry
John shot Harry .
(S (TYPE DECLARE)
(SUBJ (NP (NPR John)))
(VP (TNS PAST) (V shoot) (OBJ (NP (NPR Harry)))))
*John was shot
someone shot John .
(S (TYPE DECLARE)
(SUBJ (NP (PRO someone)))
(VP (TNS PAST) (V shoot) (OBJ (NP (NPR John)))))
*John was shot by Harry
Harry shot John .
(S (TYPE DECLARE)
(SUBJ (NP (NPR Harry)))
(VP (TNS PAST) (V shoot) (OBJ (NP (NPR John)))))
*John was believed to have been shot
someone believed that someone had shot John .
(S (TYPE DECLARE)
(SUBJ (NP (PRO someone)))
(VP (TNS PAST)
(V believe)
(OBJ (S (TYPE DECLARE)
(SUBJ (NP (PRO someone)))
(VP (TNS (PAST PERFECT))
(V shoot)
(OBJ (NP (NPR John))))))))
*John was believed to have been shot by Harry
Harry believed that someone had shot John .
(S (TYPE DECLARE)
(SUBJ (NP (NPR Harry)))
(VP (TNS PAST)
(V believe)
(OBJ (S (TYPE DECLARE)
(SUBJ (NP (PRO someone)))
(VP (TNS (PAST PERFECT))
(V shoot)
(OBJ (NP (NPR John))))))))
someone believed that Harry had shot John .
(S (TYPE DECLARE)
(SUBJ (NP (PRO someone)))
(VP (TNS PAST)
(V believe)
(OBJ (S (TYPE DECLARE)
(SUBJ (NP (NPR Harry)))
(VP (TNS (PAST PERFECT))
(V shoot)
(OBJ (NP (NPR John))))))))
*was Harry believed to have shot John
someone believed that Harry had shot John?
(S (TYPE QUESTION)
(SUBJ (NP (PRO someone)))
(VP (TNS PAST)
(V believe)
(OBJ (S (TYPE DECLARE)
(SUBJ (NP (NPR Harry)))
(VP (TNS (PAST PERFECT))
(V shoot)
(OBJ (NP (NPR John))))))))
*Jim shot John
I don't know what 'Jim' means.
[DSKLOG finished: 5-20-80 3:29 AM]
The example presented in this section couples the ATN domain with a relational database domain (RDB). The structure of the domains used to model the domain of natural language relational databases is given in figure 31. The model for the database is the DEDUCE database system [Chang76, Chang78].
The ATN can build fact and query transactions for nouns and the relationships between nouns. The dictionary specifies the specific domain in which the database operates. If the dictionary were changed to contain parts, part suppliers, part numbers, parts in assemblies, and part descriptions, then the same ATN and relational database could be used to transact about parts. Only the new dictionary would have to be refined. If a database which could deal with transactions other than relationships between nouns were desired, then the ATN would have to be modified. The relational database mechanism would only need to be re-refined if a different implementation were desired.
DICTIONARY BLOCKS
;
; This is the dictionary for the blocks world RDB
;
; NOUN = noun may imply a restriction
; NPR = indicates nomitive pronoun
; NUM = number of the noun
; TYPE = indicates a restriction
; ROOT = gives the type restriction
Fred | NOUN | NPR NUM:SINGULAR
Ethel | NOUN | NPR NUM:SINGULAR
Ricky | NOUN | NPR NUM:SINGULAR
Lucy | NOUN | NPR NUM:SINGULAR
LilRick | NOUN | NPR NUM:SINGULAR
object | NOUN | NUM:SINGULAR ROOT:OBJECT
objects | NOUN | NUM:PLURAL ROOT:OBJECT
block | NOUN | NUM:SINGULAR TYPE ROOT:BLOCK
blocks | NOUN | NUM:PLURAL TYPE ROOT:BLOCK
pyramid | NOUN | NUM:SINGULAR TYPE ROOT:PYRAMID
pyramids| NOUN | NUM:PLURAL TYPE ROOT:PYRAMID
; VERB = verb implies a relation
; NUM = number of the verb
; REL = verb relation name
; SDOM = subject domain in relation
; ODOM = object domain in relation
is | VERB | NUM:SINGULAR SDOM:OBJ ODOM:TYPE REL:IS
are | VERB | NUM:PLURAL SDOM:OBJ ODOM:TYPE REL:IS
support | VERB | NUM:PLURAL SDOM:BOT ODOM:TOP REL:SUPPORTS
supports| VERB | NUM:SINGULAR SDOM:BOT ODOM:TOP
REL:SUPPORTS
; DET = determiner implies a predicate
; DEFINITE or INDEFINITE
a | DET | INDEFINITE
an | DET | INDEFINITE
the | DET | DEFINITE
; ADJ = adjective implies a relation restriction
red | ADJ | DOM:COLOR
blue | ADJ | DOM:COLOR
green | ADJ | DOM:COLOR
; NUMBER = the numerals used as determiners
; VALUE = the numerical value
two | NUMBER| VALUE:2
three | NUMBER| VALUE:3
four | NUMBER| VALUE:4
; ATN Commands
find | CMD |
what | CMD |
how | CMD |
many | CMD |
; ATN Quantifiers
exactly | QUANT |
at | QUANT |
most | QUANT |
no | QUANT |
which | QUANT |
.END
Instead of building syntax trees, the ATN shown below builds nested transactions for the relational database system. The representation of the transactions must be the same for the two domains. The meaning of the transactions is given in [Chang76].
ATN NOUN-QUERY
NETWORK RELATIONAL-DATA-BASE
;
; ATN for questions about nouns and their relations
;
;-----------------------------------------------------------
RELATIONAL-DATA-BASE
+FACT | is word NPR ? | S:=word
; ------------------------------------------------------
QUERY | none | JVAR:='ANS
| | JVAR|:=JVAR
;-----------------------------------------------------------
FACT +F1 | class VERB? | REL:=word[REL]
| word[NUM]='SINGULAR | F:=('FACT REL
(word[SDOM] S))
| | OD:=word[ODOM]
;-----------------------------------------------------------
F1 +FOUT | is word NPR ? | <=#F+((OD word))
; ------------------------------------------------------
+FOUT | class ADJ? | <=#F+((word[DOM] word))
| REL='IS |
; ------------------------------------------------------
+F2 | class DET? | none
| is word INDEFINITE ?|
;-----------------------------------------------------------
F2 +F2 | class ADJ? | F:=F+((word[DOM] word))
; ------------------------------------------------------
F3 | class NOUN? | none
| word[NUM]='SINGULAR |
| REL='IS |
;-----------------------------------------------------------
F3 +FOUT | is word TYPE ? |<=#F+(('TYPE word[ROOT]))
; ------------------------------------------------------
+FOUT | word[ROOT]='OBJECT | <=F
;-----------------------------------------------------------
FOUT exit | none | none
;-----------------------------------------------------------
QUERY +FQ | word='find | none
; ------------------------------------------------------
+WQ | word='what | none
; ------------------------------------------------------
+HQ | word='how | none
;-----------------------------------------------------------
FQ FQ1 | none | D<=DET
| | JVAR|:=JVAR
| | N<=NOUN-PHRASE
;-----------------------------------------------------------
FQ1 exit | N[NUM]=D[NUM] | <=('QUERY
('RESULT 'ANS)
('SUBQUERY
('RESULT 'ANS))
+N[FORMS]
('PREDICATE
(D[OP]
('COUNT 'ANS)
D[OPN])))
;-----------------------------------------------------------
WQ exit | none | Q<=NPVP
| | <=('QUERY
('RESULT 'ANS))
+Q
;-----------------------------------------------------------
HQ +HQ1 | word='many | none
;-----------------------------------------------------------
HQ1 exit | none | Q<=NPVP
| | <=('QUERY
('RESULT 'COUNT)
('SUBQUERY
('RESULT 'ANS))
+Q
('COMPUTE 'COUNT
('COUNT 'ANS)))
;-----------------------------------------------------------
NPVP NV1 | none | JVAR|:=JVAR
| | N<=NOUN-PHRASE
| | JVAR|:=JVAR
| | V<=VERB-PHRASE
;-----------------------------------------------------------
NV1 exit | N[NUM]=V[NUM] | <=#N[FORMS]+V[FORMS]
;-----------------------------------------------------------
NOUN-PHRASE
NP1 | none | REL:=('RELATION 'IS
('BIND 'OBJ
JVAR))
;-----------------------------------------------------------
NP1 +NP1 | class ADJ? | RS:=RS+(('RESTRICT
word[DOM]
word))
; ------------------------------------------------------
NP2 | class NOUN? | A[NUM]:=word[NUM]
;-----------------------------------------------------------
NP2 +NP3 | is word TYPE ? | RS:=RS+(('RESTRICT 'TYPE
word[ROOT]))
; ------------------------------------------------------
+NP3 | is word NPR ? | RS:=RS+(('RESTRICT 'OBJ
word))
; ------------------------------------------------------
+NP3 | word[ROOT]='OBJECT | none
;-----------------------------------------------------------
NP3 +NP4 | word='which | none
; ------------------------------------------------------
exit | none | A[FORMS]:=(REL+RS)
| | <=A
;-----------------------------------------------------------
NP4 NP5 | none | JVAR|:=JVAR
| | V<=VERB-PHRASE
;-----------------------------------------------------------
NP5 exit | V[NUM]=A[NUM] | A[FORMS]:= (REL+RS)
+V[FORMS]
| | <=A
;-----------------------------------------------------------
VERB-PHRASE
+VP1 | class VERB? | A[NUM]:=word[NUM]
| | REL:=word[REL]
| | SD:=word[SDOM]
| | OD:=word[ODOM]
;-----------------------------------------------------------
VP1 VP2 | none | D<=DET
| | NVAR:=symbol
| | JVAR|:=NVAR
| | N<=NOUN-PHRASE
;-----------------------------------------------------------
VP2 exit | D[NUM]=N[NUM] | SQ:=('SUBQUERY
('RELATION REL
('BIND SD JVAR)
('REPORT OD
NVAR)))+N[FORMS]
| | PRED:=('PREDICATE
(D[OP]
('COUNT NVAR)
D[OPN]))
| | A[FORMS]:=(SQ PRED)
| | <=A
;-----------------------------------------------------------
DET +D3 | class DET? | D[NUM]:='SINGULAR
| is word INDEFINITE ?| D[OP]:='GE
| | D[OPN]:=0
; ------------------------------------------------------
+D3 | class DET? | D[NUM]:='SINGULAR
| is word DEFINITE ? | D[OP]:='EQ
| | D[OPN]:=1
; ------------------------------------------------------
+D3 | class NUMBER? | D[NUM]:='PLURAL
| | D[OP]:='GE
| | D[OPN]:=word[VALUE]
; ------------------------------------------------------
+D3 | word='no | D[NUM]:='PLURAL
| | D[OP]:='EQ
| | D[OPN]:=0
; ------------------------------------------------------
+D2 | word='exactly | D[OP]:='EQ
; ------------------------------------------------------
+D1 | word='at | none
;-----------------------------------------------------------
D1 +D2 | word='most | D[OP]:='LE
;-----------------------------------------------------------
D2 +D3 | class NUMBER? | D[NUM]:='PLURAL
| | D[OPN]:=word[VALUE]
;-----------------------------------------------------------
D3 exit | none | <=D
;-----------------------------------------------------------
.END
The sample executions below take in a sentence and show the database transaction formed. The database response is a set of sets denoted by parentheses.
[DSKLOG started: 5-20-80 3:36 AM]
*(TESTER)
RDB input : *Fred is a red block
(FACT IS (OBJ Fred) (COLOR red) (TYPE BLOCK))
OK
RDB input : *Ethel is a green block
(FACT IS (OBJ Ethel) (COLOR green) (TYPE BLOCK))
OK
RDB input : *Ricky is a red pyramid
(FACT IS (OBJ Ricky) (COLOR red) (TYPE PYRAMID))
OK
RDB input : *Lucy is a green pyramid
(FACT IS (OBJ Lucy) (COLOR green) (TYPE PYRAMID))
OK
RDB input : *Fred supports Ethel
(FACT SUPPORTS (BOT Fred) (TOP Ethel))
OK
RDB input : *Ricky supports Lucy
(FACT SUPPORTS (BOT Ricky) (TOP Lucy))
OK
RDB input : *Ricky supports Ethel
(FACT SUPPORTS (BOT Ricky) (TOP Ethel))
OK
RDB input : *find a pyramid
(QUERY (RESULT ANS)
(SUBQUERY (RESULT ANS)
(RELATION IS
(BIND OBJ ANS)
(RESTRICT TYPE PYRAMID)))
(PREDICATE (GE (COUNT ANS) 0)))
response =
(((Lucy Ricky)))
RDB input : *find a red pyramid
(QUERY (RESULT ANS)
(SUBQUERY (RESULT ANS)
(RELATION IS
(BIND OBJ ANS)
(RESTRICT COLOR red)
(RESTRICT TYPE PYRAMID)))
(PREDICATE (GE (COUNT ANS) 0)))
response =
(((Ricky)))
RDB input : *find a pyramid which supports a block
(QUERY (RESULT ANS)
(SUBQUERY (RESULT ANS)
(RELATION IS
(BIND OBJ ANS)
(RESTRICT TYPE PYRAMID))
(SUBQUERY (RELATION SUPPORTS
(BIND BOT ANS)
(REPORT TOP G0158))
(RELATION IS
(BIND OBJ G0158)
(RESTRICT TYPE BLOCK))
)
(PREDICATE (GE (COUNT G0158) 0)))
(PREDICATE (GE (COUNT ANS) 0)))
response =
(((Ricky)))
RDB input : *find the block which supports a block
(QUERY (RESULT ANS)
(SUBQUERY (RESULT ANS)
(RELATION IS
(BIND OBJ ANS)
(RESTRICT TYPE BLOCK))
(SUBQUERY (RELATION SUPPORTS
(BIND BOT ANS)
(REPORT TOP G0159))
(RELATION IS
(BIND OBJ G0159)
(RESTRICT TYPE BLOCK))
)
(PREDICATE (GE (COUNT G0159) 0)))
(PREDICATE (EQ (COUNT ANS) 1)))
response =
(((Fred)))
RDB input : *how many blocks support a pyramid
(QUERY (RESULT COUNT)
(SUBQUERY (RESULT ANS)
(RELATION IS
(BIND OBJ ANS)
(RESTRICT TYPE BLOCK))
(SUBQUERY (RELATION SUPPORTS
(BIND BOT ANS)
(REPORT TOP G0160))
(RELATION IS
(BIND OBJ G0160)
(RESTRICT TYPE PYRAMID
)))
(PREDICATE (GE (COUNT G0160) 0)))
(COMPUTE COUNT (COUNT ANS)))
response =
NONE
RDB input : *how many pyramids support a block
(QUERY (RESULT COUNT)
(SUBQUERY (RESULT ANS)
(RELATION IS
(BIND OBJ ANS)
(RESTRICT TYPE PYRAMID))
(SUBQUERY (RELATION SUPPORTS
(BIND BOT ANS)
(REPORT TOP G0161))
(RELATION IS
(BIND OBJ G0161)
(RESTRICT TYPE BLOCK))
)
(PREDICATE (GE (COUNT G0161) 0)))
(COMPUTE COUNT (COUNT ANS)))
response =
((1))
RDB input : *find a pyramid which is green
I do not understand
*(LOGOUT)
[DSKLOG finished: 5-20-80 3:44 AM]